Предмет: Математика,
автор: orcieresk
Помогите, пожалуйста, с решением!
Найти все значения параметра а, при которых система имеет единственное решение:
х^2 - 2у=а,
х+у=а
Приложения:

Ответы
Автор ответа:
1
Выразим заданные уравнения относительно у:

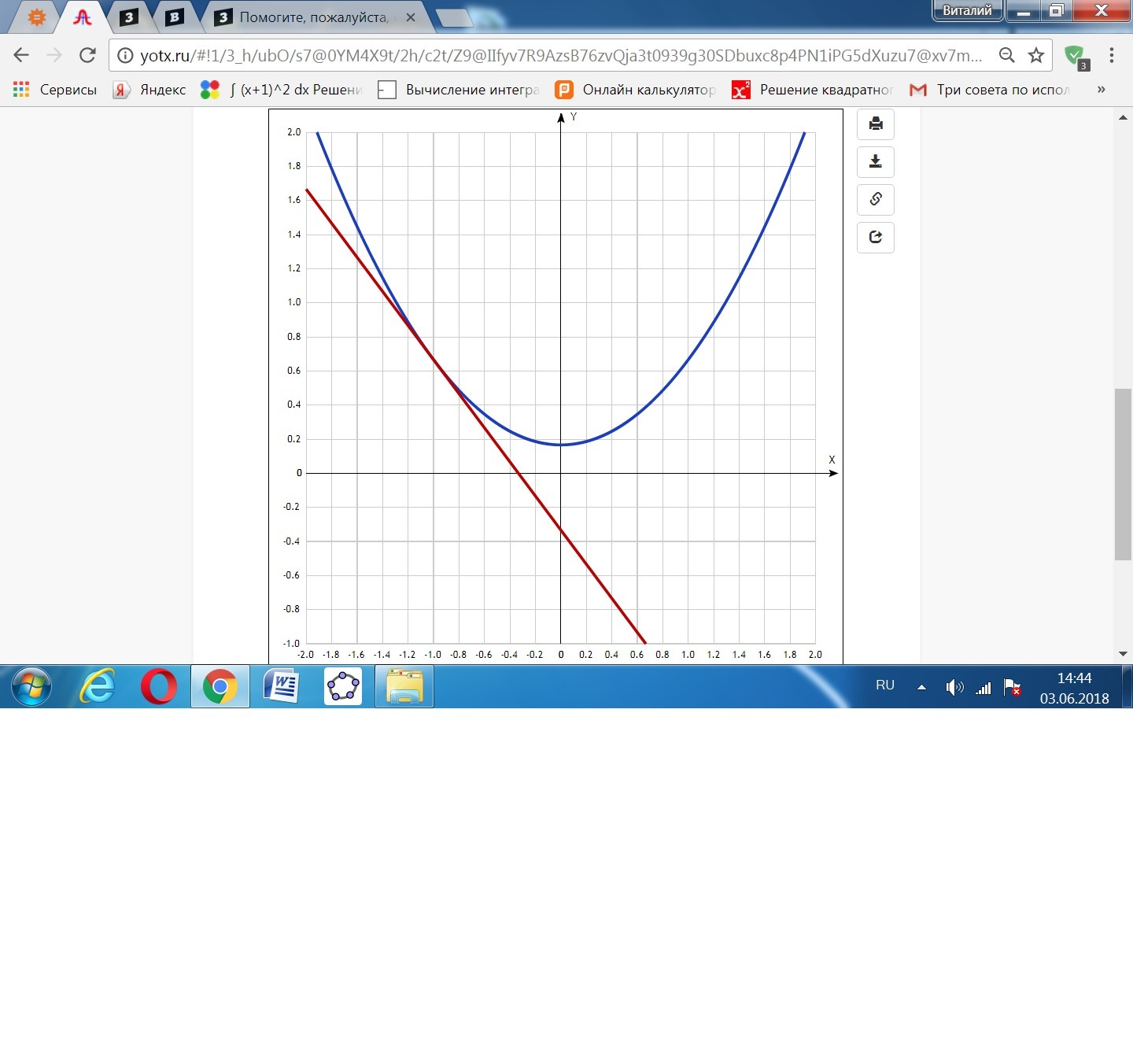
Как видим, система представлена параболой, симметричной оси Оу с вершиной на этой оси в точке (0; (-а/2)), и прямой с к=-1, пересекающей ось Оу в точке (0; а).
Единственным решением системы является точка касания прямой и параболы.
Приравняем функции:

Получаем квадратное уравнение: х² + 2х - 3а = 0.
Дискриминант Д = 4 + 12а.
Приравниваем его нулю, чтобы уравнение имело единственное решение:
4 + 12а = 0,
а = -4/12 = -1/3.
Получаем:
- уравнение параболы у = (1/2)х² + (1/6),
- прямой у = -х - (1/3).
Как видим, система представлена параболой, симметричной оси Оу с вершиной на этой оси в точке (0; (-а/2)), и прямой с к=-1, пересекающей ось Оу в точке (0; а).
Единственным решением системы является точка касания прямой и параболы.
Приравняем функции:
Получаем квадратное уравнение: х² + 2х - 3а = 0.
Дискриминант Д = 4 + 12а.
Приравниваем его нулю, чтобы уравнение имело единственное решение:
4 + 12а = 0,
а = -4/12 = -1/3.
Получаем:
- уравнение параболы у = (1/2)х² + (1/6),
- прямой у = -х - (1/3).
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sasasalutova
Предмет: Другие предметы,
автор: dariaufimcuk
Предмет: Математика,
автор: ivanplotnikov228
Предмет: Информатика,
автор: Аноним
Предмет: Биология,
автор: RollingStone