Предмет: Геометрия,
автор: 1nnnnnn11
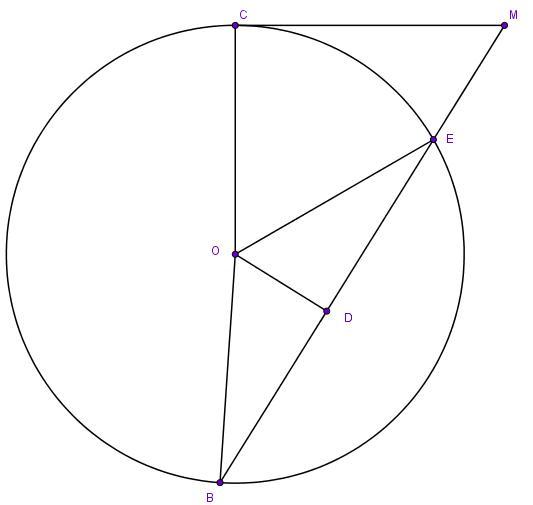
Дана окружность (O;OC). Из точки M, которая находится вне окружности, проведена секущая MB и касательная MC.
OD — перпендикуляр, проведённый из центра окружности к секущей MB и равный 8 см.
Найди радиус окружности, если известно, что MB равен 40 см и MC равен 20 см.
Ответ: радиус равен (целое число) см
Ответы
Автор ответа:
5
По теореме о секущей и касательной:
см
Тогда см. OB = OE как радиусы окружности, следовательно, ΔBOE - равнобедренный, OD - высота, медиана и биссектриса, значит BD = DE = 15 см. По теореме Пифагора из прямоугольного треугольника BOD:
см
Ответ: 17 см.
Приложения:
Похожие вопросы
Предмет: История,
автор: dimadedula674
Предмет: Математика,
автор: shinkis
Предмет: Обществознание,
автор: milanasaviceva0
Предмет: Математика,
автор: SSN90
Предмет: Математика,
автор: Аноним