Question

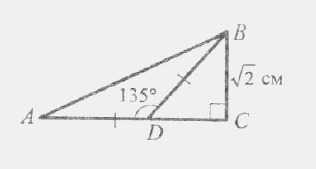
Знайдіть площу трикутника ABC, зображеного на рисунку

Answer 1

1) Угол BDC = 180° - угол ADB = 180° - 135° = 45° (смежные углы)
2) Угол DBC = 180° - 90° - угол BDC = 180° - 90° - 45° = 45°
3) Углы DBC и BDC равны, значит, треугольник DBC - равнобедренный, тогда BC = DC = √2 см
4) По теореме Пифагора:
BD = $\sqrt{DC^2+BC^2}$ = $\sqrt{ \sqrt{ 2 } ^2 + \sqrt{2}^2 }$ = $\sqrt{2+2}$ = $\sqrt{4}$ = 2
5) BD = AD (условия)
AC = AD + DC = 2 + √2 см
6) S = 1/2 * AC * BC = (2 + √2)*√2 / 2 = 2√2 + 2 / 2 = 2(√2 + 1) / 2 = √2 + 1
Ответ : площадь равна √2 + 1

Answer 2

∠BDC = 180 - 135 = 45° (смежные углы)
∠DBC = 90 - 45 = 45° (сумма острых углов прямоуг.Δ = 90°)
Следовательно, ΔВСD - равнобедренный ⇒
СD = BC = √2 cм

Найдем ВD по теореме Пифагора:
ВD² = ВС² + СD²
ВD² = (√2)² + (√2)²
ВD² = 2 + 2
ВD² = 4
ВD = 2 cм

AD = BD = 2 cм (по условию)

AC =  AD + CD = 2+ √2

Найдем площадь:

$S_{ABC}= \cfrac{BC\cdot AC}{2}= \cfrac{ \sqrt{2}\cdot(2+ \sqrt{2} )}{2}=\cfrac{ 2 \sqrt{2}+2 }{2}=\cfrac{ 2(\sqrt{2}+1) }{2}= \sqrt{2}+1$

Ответ: (√2+1) см²