Question

Ассаламу алейкум помогите пожалуйста...
1. Доказать:
Теорему о внешнем угле
Признаки параллельности прямых
Построение центра круга
Описание окружности около треугольника

Буду очень благодарен, если решите хотя бы что-то. Даю 25 баллов.

Answer 1

Теорема о внешнем угле
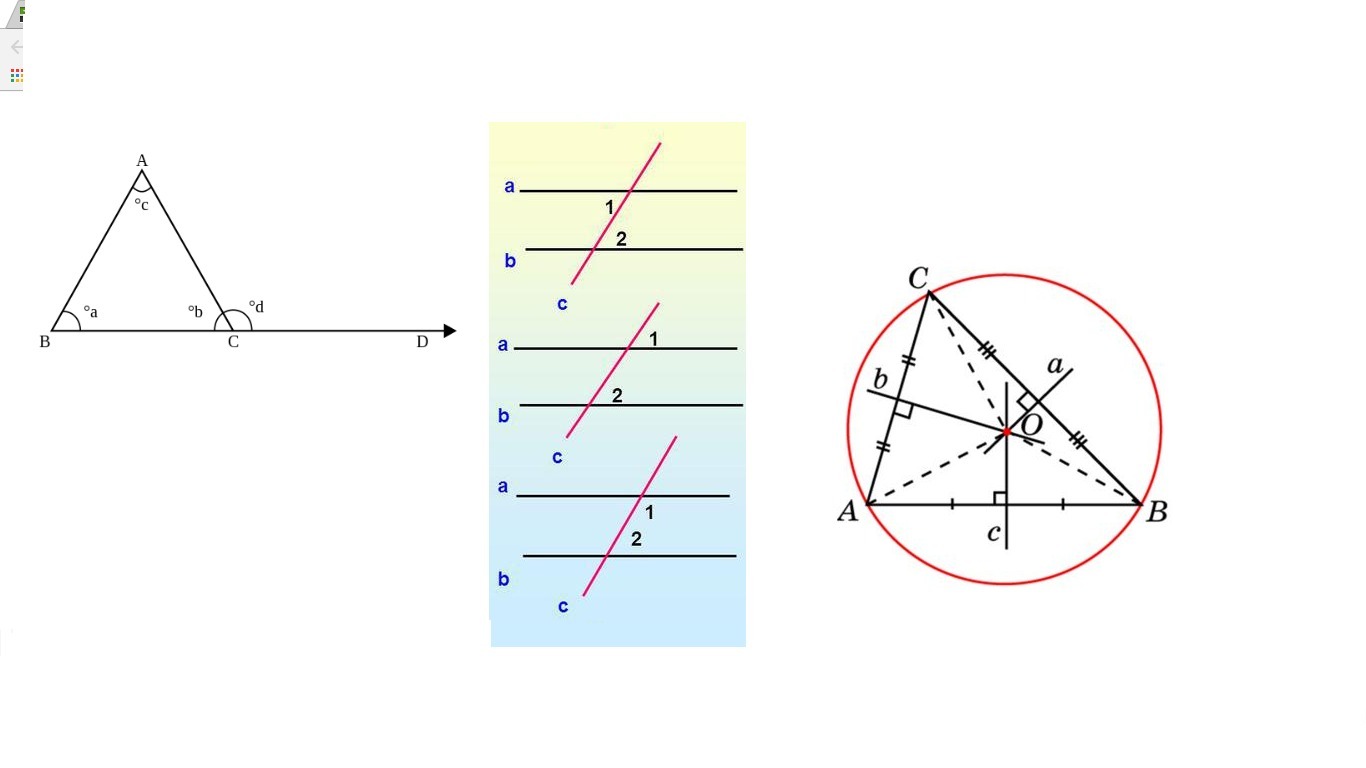
Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.
Пусть АВС - произвольный треугольник с внешним углом d. Так как углы b и d смежные , то d = 180 - b.
По теоремем о сумме углов трегольника b = 180 - (a+c)
Получаем d = 180 - b = 180 - (180 - (a+c)) = a+c
Что и требовалось доказать.

Признаки параллельности прямых
- если внутренние накрест лежащие углы равны, то прямые параллельны
 - если соответственные углы равны, то прямые параллельны
 - если сумма внутренних односторонних углов равно 180, то прямые параллельны
 - если две прямые параллельны третьей, то они и параллельны между собой.

Описание окружности около треугольника
Около любого треугольника можно описать окружность. Центр описанной окружности - это точка пересечения серединных перпендикуляров, проведенных к сторонам.