Предмет: Алгебра, автор: ashugalskij

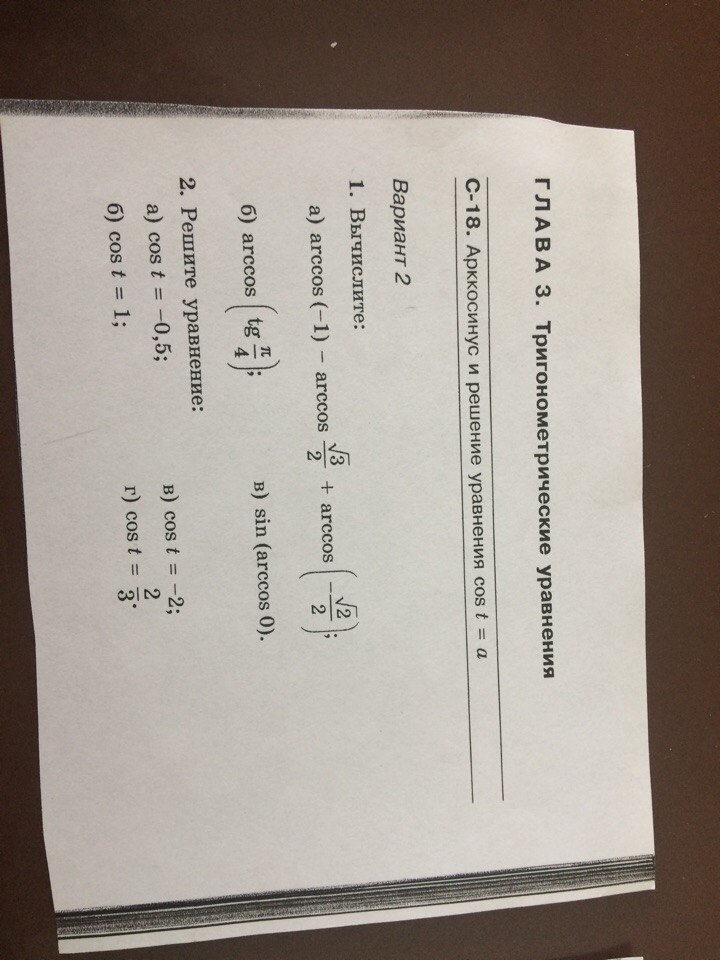
Помогите пожалуйста

Приложения:

Аноним: Здравствуй! 1. нужно смотреть в тригонометрическую таблицу затем описать частный случай -1 вместо этого замените чему равен -1 так же для другого так же другое уравнение пи n, т принадлежит z только у тебя не это другое просмотри частный случай arc -обратная то есть обратная тригонометрическая функция sin(-3) будет arcsin(-3)+пи n т принадлежит z отсальный так же

Аноним: в б там наоборот tg пи/4 замени на число если этого нету в таблице то разложи tg как sin и cos

vladoleyp8x2va: все тригонометрические функции берутся по таблице, ее можно посмотреть здесь ru.onlinemschool.com/math/formula/sine_table/
и не валите все в кучу, лучше сделайте много заданий по одной задаче =)

Аноним: Здравствуй! разве не говорил про таблицу

Ответы

Автор ответа: vladoleyp8x2va

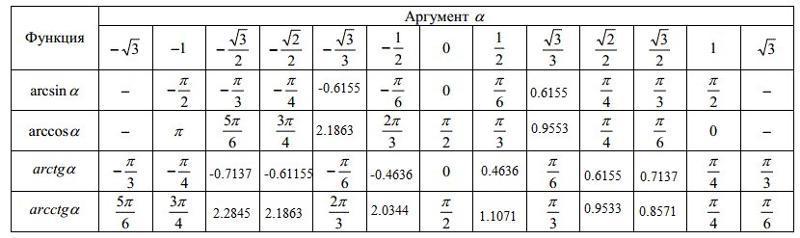
Посмотрим таблицу :
otvet . imgsmail . ru /download/212520366_1e57a2e963deb19ee1b4cafb0f9426b7_800.jpg
Все функции периодичны, поэтому в ответе дописываем период 2π*n или n*π, где n∈Z
arcctg(-1) = 3/4 * π + n*π
arcctg(0) = 1/2 * π + n*π
arcctg(√3 / 3) = 1/3 * π + n*π
С-20
1 a) подставим и посчитаем 3/4 * π + 1/3 * π + 1/2 * π = 19/12 * π + n*π
1 б) 1/√2 если умножить числитель и знаменатель на √2 то 1/√2 = √2/2
arccos(1/√2) = arccos(√2/2) = 1/4 * π по таблице
ctg( arccos(1/√2) ) = ctg( 1/4 * π ) = 1
1 в) arctg( cos(π) ) = arctg( -1 ) = -1/4 * π + n*π
2 a) ctg(x) = -1
x = arcctg(-1) = 3/4 * π + n*π
2 б) tg(x) = 1/6 т.к. нет табличного такого тангенса, то просто пишем арктангенс 1/6
x = arctg(1/6) + n*π

Приложения: