Предмет: Геометрия,
автор: smolayaroslav
Треугольник АВС- равносторонний. Высота ВН равна 12. Найдите расстояние от точки Н до стороны ВС.
Решите пожалуйста. Даю 80 баллов.
Ответы
Автор ответа:
0
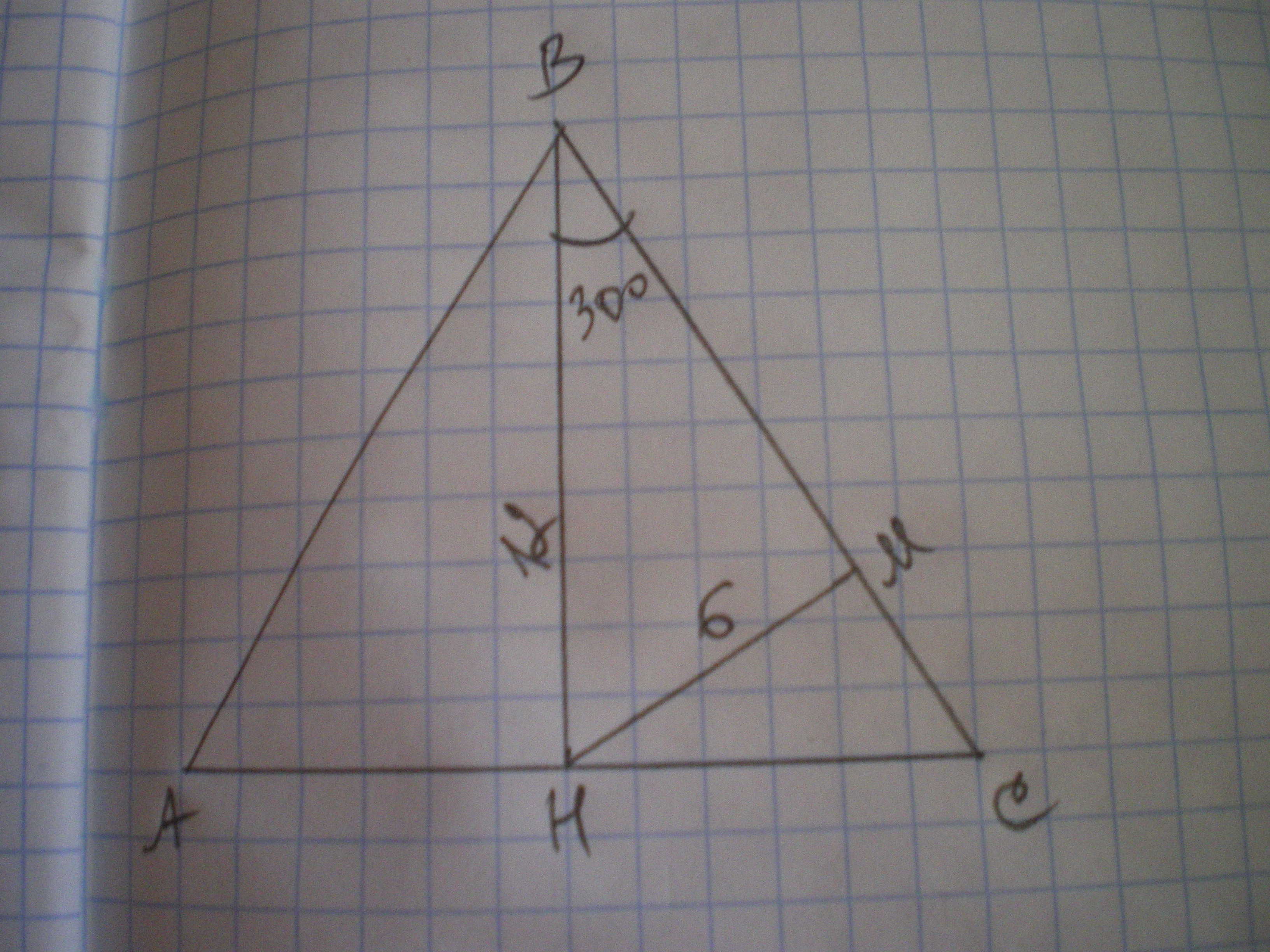
Дано: ΔАВС - равносторонний, ВН - высота, ВН=12.
Найти НМ.
В равностороннем треугольнике все углы равны 60°.
Рассмотрим ΔВНС - прямоугольный.
∠СВН=1\2 ∠В=30°, т.к. в равностороннем треугольнике высота является и биссектрисой угла.
МН в данном треугольнике является высотой, потому что перпендикуляр - кратчайшее расстояние от точки до прямой.
ΔВМН - прямоугольный, ∠ВМН=90°, ∠МВН=30°, значит,
МН=1\2 ВН=12:2=6 (ед.)
Ответ: 6 ед.
Найти НМ.
В равностороннем треугольнике все углы равны 60°.
Рассмотрим ΔВНС - прямоугольный.
∠СВН=1\2 ∠В=30°, т.к. в равностороннем треугольнике высота является и биссектрисой угла.
МН в данном треугольнике является высотой, потому что перпендикуляр - кратчайшее расстояние от точки до прямой.
ΔВМН - прямоугольный, ∠ВМН=90°, ∠МВН=30°, значит,
МН=1\2 ВН=12:2=6 (ед.)
Ответ: 6 ед.
Приложения:
Автор ответа:
0
КН⊥ВС. ВН=12. ΔВСН- прямоугольный, Подобный египетскому треугольнику с коэффициентом подобия k=12/4=3 Стороны египетского треугольника 3; 4;5. Стороны ΔВСН равныВН-12; СН=3·3=9; ВС=15.
Пусть СК==, тогда ВК=15-х
ΔСНК. НК²=СН²-СК²=81-х².
ΔВНК. НК²=ВН²-ВК²=12²-(15-х)²=144-225+30х-х²=-81+30х-х².
81-х²=-81+30х-х²;
30х=162,
х=162/30=5,4; КС=5,4: ВК=15-5,4=9,6;
h²=5,4·9,6=51,84;
h=√51,84=7,2. НК=7,2.
Пусть СК==, тогда ВК=15-х
ΔСНК. НК²=СН²-СК²=81-х².
ΔВНК. НК²=ВН²-ВК²=12²-(15-х)²=144-225+30х-х²=-81+30х-х².
81-х²=-81+30х-х²;
30х=162,
х=162/30=5,4; КС=5,4: ВК=15-5,4=9,6;
h²=5,4·9,6=51,84;
h=√51,84=7,2. НК=7,2.
Приложения:
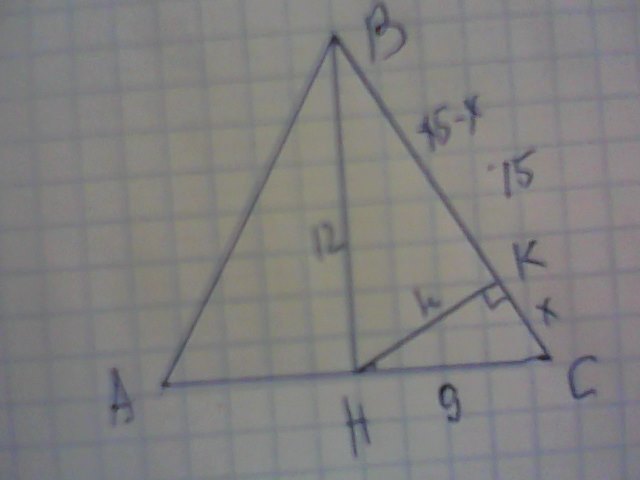
Похожие вопросы
Предмет: Физика,
автор: evgjeniy
Предмет: Математика,
автор: Nionli
Предмет: Математика,
автор: Sek34
Предмет: Химия,
автор: Lizuuuuuuunya
Предмет: Литература,
автор: grudyankina