Предмет: Геометрия, автор: Денис258грг

в прямоугольном треугольнике A C B провели высоту СМ угол C 90 градусов угол B 30 градусов АВ гипотенуза равна 10 см найти Чему равно BM

Andr1806: Дополнительные требования к задаче надо указывать в условии.

Ответы

Автор ответа: Пеппер

Дано: ΔАВС - прямоугольный, ∠С=90°, ∠В=30°, АВ=10 см, СМ - высота.
Найти ВМ.

АС=1\2 АВ = 5 см как катет, лежащий против угла 30°.
ВС=√(АВ²-АС²)=√(100-25)=√75=5√3 см.
СМ=1\2 ВС = 2,5√3 см.
ВМ²=ВС²-СМ²=75-18,75=56,25
ВМ=7,5 см.

Денис258грг: что за галочки что за квадраты у меня 7 класс а не 8-11 классы я не понял что написано

Денис258грг: Большое спасибо Ведущему за отличный ответ

Автор ответа: Andr1806

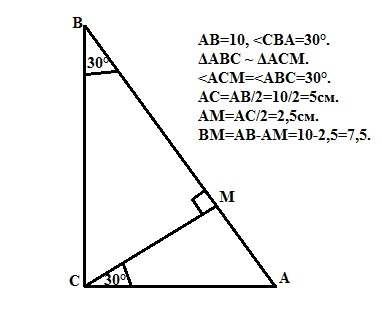
В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два меньших треугольника, подобных исходному и подобных друг другу. Отсюда угол МСА равен углу СВА, то есть
<MCA=<CBA=30° (дано).
Против угла 30° лежит катет, равный половине гипотенузы.
Поэтому катет АС = 10:2 = 5 см.
В треугольнике СМА <MCA=30°, поэтому катет МА равен половине гипотенузы СА. МА=5:2=2,5 см.
Тогда ВМ=ВА-МА = 10-2,5 =7,5 см.
Ответ: ВМ=7,5 см.

Приложения: