Предмет: Геометрия,
автор: anastasia280204
в равнобокую трапецию вписана окружность с радиусом 12 см одна из боковых сторон точкой касания делится на 2 отрезка больший из которых равен 16 см найдите площадь трапеции
Ответы
Автор ответа:
8
Высота трапеции равна диаметру вписанной окружности.
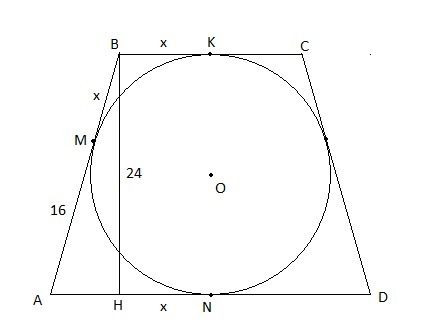
BH = 24; AM = AN = 16; MB = BK = HN = x;
AB = 16 + x; AH = 16 – x.
По теореме Пифагора:
(16 + х)² − (16 - x)² = 24²
(16² + 32x + x²) – (16² − 32x + x²) = 576
64x = 576
x = 576 : 64 = 9
AB = 16 + 9 = 25
Если в трапецию вписана окружность, то сумма оснований трапеции равна сумме боковых сторон.
AD + BC = 50
S = 50 * 24 : 2 = 600 см².
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: elsujertolkyn
Предмет: Математика,
автор: Audi3491
Предмет: Математика,
автор: shchetnikovak
Предмет: Математика,
автор: iiss
Предмет: Биология,
автор: Агнесбожий