Предмет: Алгебра,
автор: pacixor
Задание во вложении..
Приложения:
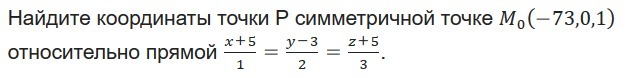
viva34:
лень писать
убери _
Ответы
Автор ответа:
1
1. Находим уравнение плоскости, которая перпендикулярна данной прямой и проходит через точку Мо(-73;0;1). Так как плоскость перпендикулярна заданной прямой, то в качестве ее вектора нормали можно взять направляющий вектор прямой, т.е. ñ={1;2;3}.
Поэтому уравнение плоскости будет
1(x-(-73))+2(y-0)+3(z-1)=0
x+73+2y+3z-3=0
x+2y+3z+70=0.
2. Находим точку O пересечения заданной прямой и плоскости x+2y+3z+70=0.
Запишем параметрические уравнения прямой.

Подставляем в уравнение плоскости:

Откуда координаты точки пересечения прямой и плоскости будут

О(-9;-5;-17).
3. Точка О является серединой отрезка РМо, где точка P является точкой симметричной точке Mo, поэтому

откуда

Хр=2*(-9)-(-73)=-18+73=55
Ур=2*(-5)-0=-10
Zp=2*(-17)-1=-34-1=-35
ответ: Р(55;-10;-35)
Поэтому уравнение плоскости будет
1(x-(-73))+2(y-0)+3(z-1)=0
x+73+2y+3z-3=0
x+2y+3z+70=0.
2. Находим точку O пересечения заданной прямой и плоскости x+2y+3z+70=0.
Запишем параметрические уравнения прямой.
Подставляем в уравнение плоскости:
Откуда координаты точки пересечения прямой и плоскости будут
О(-9;-5;-17).
3. Точка О является серединой отрезка РМо, где точка P является точкой симметричной точке Mo, поэтому
откуда
Хр=2*(-9)-(-73)=-18+73=55
Ур=2*(-5)-0=-10
Zp=2*(-17)-1=-34-1=-35
ответ: Р(55;-10;-35)
напиши мне в личку, тут ссылки не открываются
Похожие вопросы
Предмет: История,
автор: demidkagorokhov
Предмет: Английский язык,
автор: nurayismailzade2
Предмет: Русский язык,
автор: Harutj
Предмет: Математика,
автор: никит16
Предмет: Математика,
автор: 12345552