Question

знайти площу прямокутного трикутника якщо бісектриса прямого кута ділить гіпотенузу на відрізки завдовжки 30см і 40см

Answer 1

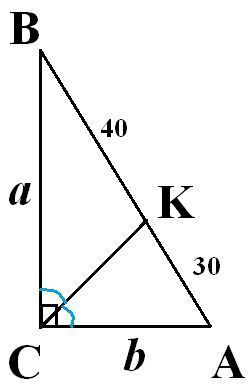
Смотрим чертеж.
Пусть АВС - прямоугольный треугольник с биссектрисой СК прямого угла С. Обозначим ВС = а и АС = b.
По свойству биссектрисы угла треугольника $\frac{BC}{BK} = \frac{AC}{AK}$
По теореме Пифагора $BC^2+AC^2=AB^2$
Из этих двух равенств получим систему уравнений:
$\begin {cases} \frac{a}{40} = \frac{b}{30} \\ a^2+b^2=70^2 \end {cases} \ \textless \ =\ \textgreater \ \begin {cases} b = \frac{3}{4}a \\ a^2+(\frac{3}{4}a)^2=70^2 \end {cases} \ \textless \ =\ \textgreater \ \\ \ \textless \ =\ \textgreater \ \begin {cases} b = \frac{3}{4}a \\ \frac{25}{16}a^2=70^2 \end {cases} =\ \textgreater \ \begin {cases} \frac{5}{4}a=70 \\ b = \frac{3}{4}a \end {cases} \ \textless \ =\ \textgreater \ \begin {cases} a=48 \\ b = 36 \end {cases}$
$S_{ABC}= \frac{1}{2} ab= \frac{1}{2}*36*48= 864$ (см²)