Question

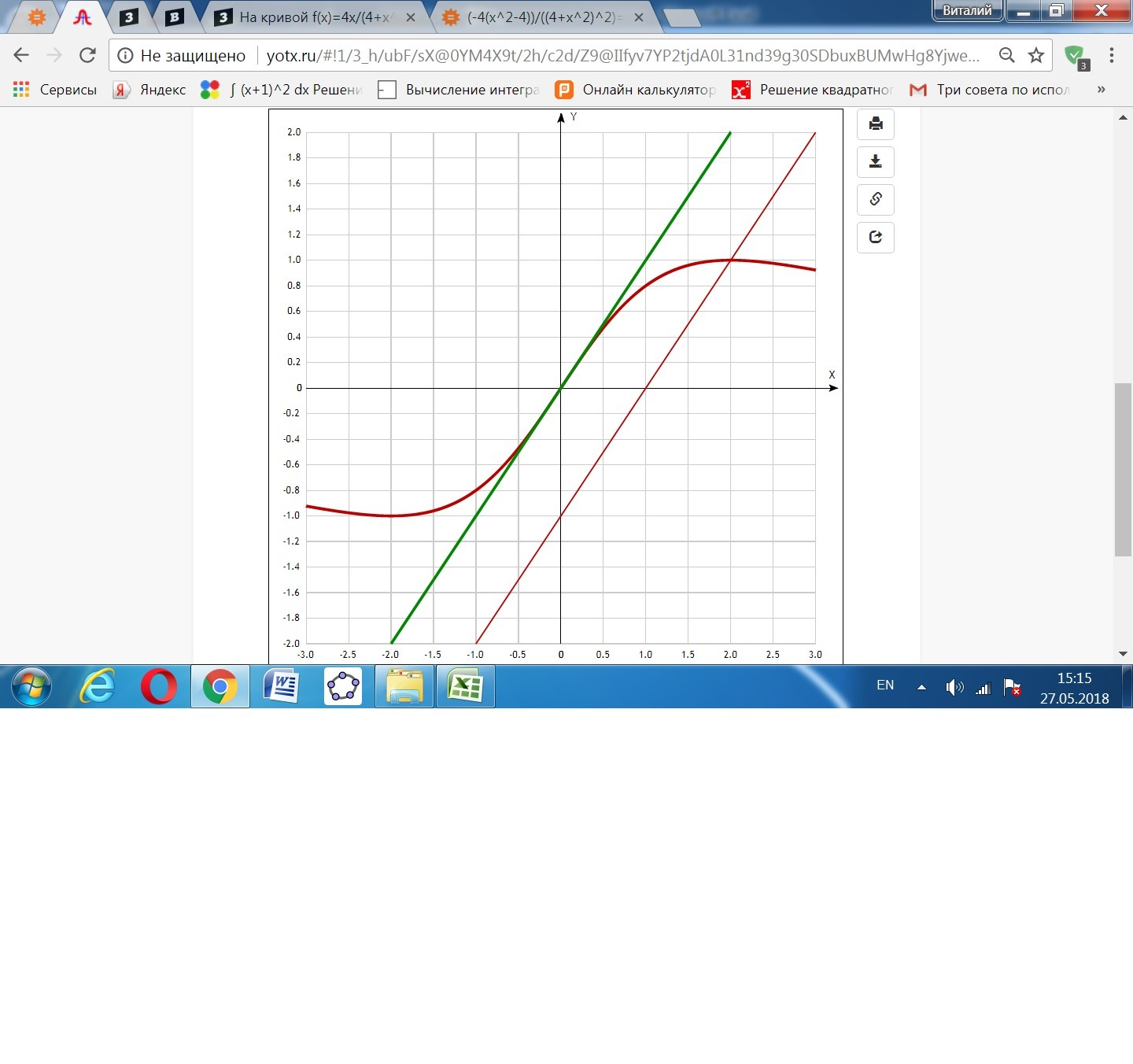
На кривой f(x)=4x/(4+x^2) найдите точку,в которой касательная параллельна прямой y=x-1

Answer 1

Дана функция f(x)=4x/(4+x²).
Найти точку,в которой касательная параллельна прямой y=x-1.

Производная этой функции равна:
y' = (-4(x²-4))/((x²+4)²).
Производная равна угловому коэффициенту а касательной в виде у = ах+в.
По заданию у прямой а = 1.
Приравниваем единице производную:
(-4(x²-4))/((x²+4)²) = 1.
-4х²+16 = x^4+8x^2+16.
x^4+12x^2 = 0
x^2(x^2+12) = 0.
Отсюда видим, что х = 0.

Ответ: искомая точка - начало координат (0; 0).