Предмет: Алгебра,
автор: jkpl
Помогите решить логарифмическое уравнение. буду очень благодарна
Приложения:
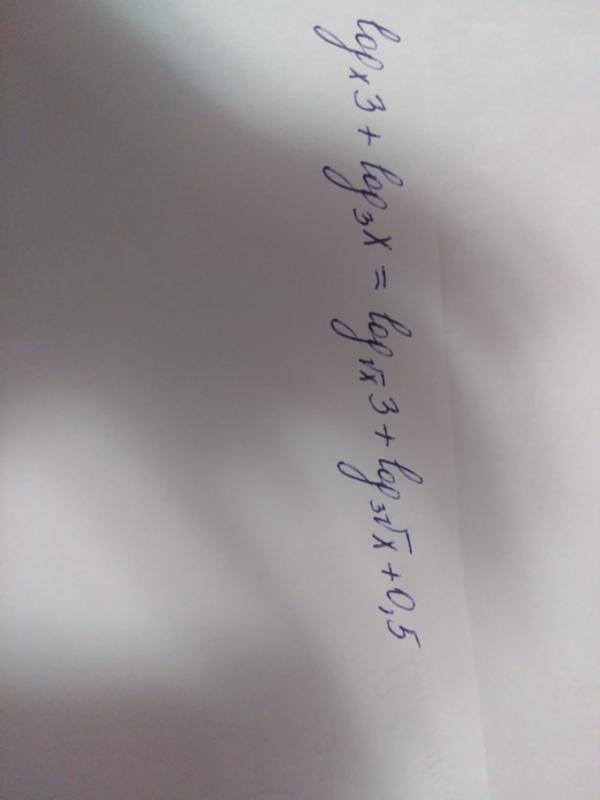
Ответы
Автор ответа:
0
ОДЗ: x > 0, x ≠ 1, √x > 0, √x ≠ 1 или x ∈ (0; 1) ∪ (1; +∞)

Замена: log₃x = t


Замена: log₃x = t
Похожие вопросы
Предмет: Математика,
автор: lalam5007
Предмет: Информатика,
автор: irunak409
Предмет: Другие предметы,
автор: IwaaaN
Предмет: Химия,
автор: sergeevanora
Предмет: Математика,
автор: Аноним