Предмет: Геометрия,
автор: dashamaz2003
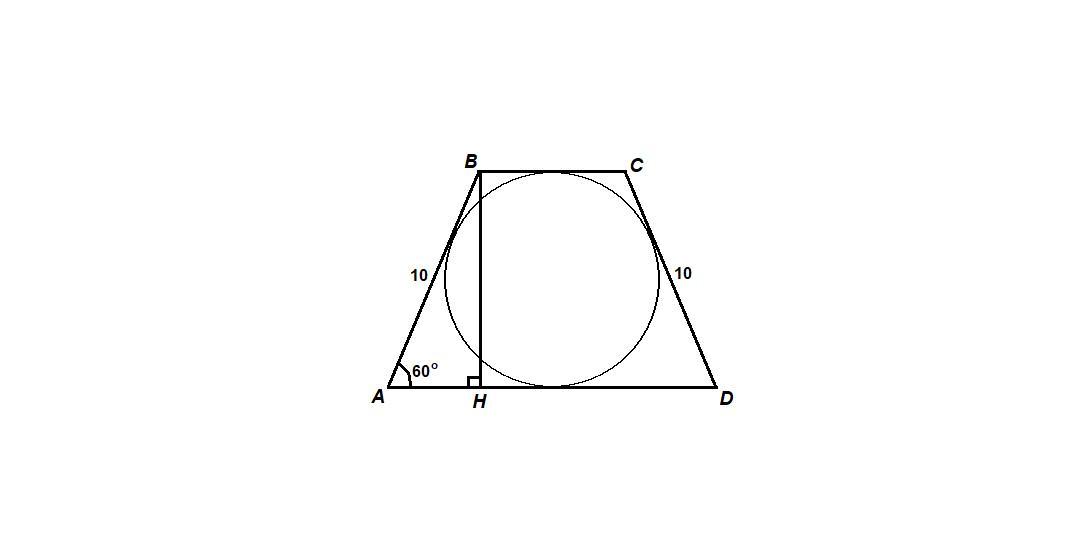
Боковая сторона равнобокой трапеции равна 10 см, а острый угол — 60°. Найдите площадь трапеции, если известно, что в неё можно вписать окружность.
Ответы
Автор ответа:
29
Ответ: 50√3 см²
Объяснение:
Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны:
AD + BC = AB + CD = 10 · 2 = 20 см
ΔАВН: ΔAHB = 90°
sin∠A = BH/AB
BH = AB · sin∠A = 10 · sin60° = 10 · √3/2 = 5√3 см
Sabcd = 0,5 · (AD + BC) · BH = 0,5 · 20 · 5√3 = 50√3 см²
Приложения:
Похожие вопросы
Предмет: Физика,
автор: daznormaz
Предмет: Математика,
автор: kareyka22
Предмет: История,
автор: hamest220209
Предмет: История,
автор: даша1590