Предмет: Математика,
автор: hosefulive
Максимально подробно опишите алгоритм сокращения дробей.
Для примера:
Приложения:
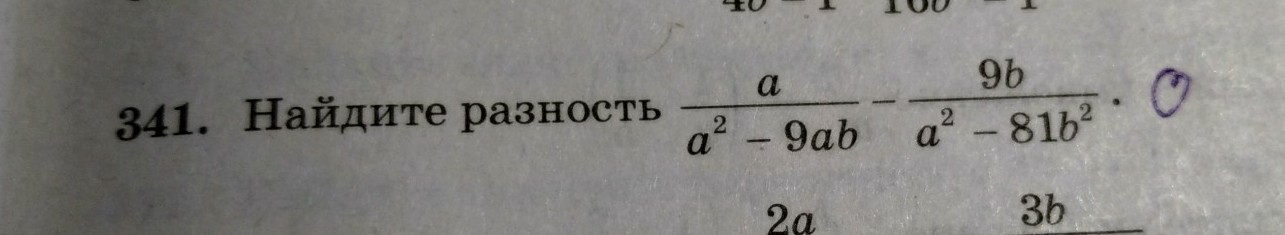
Ответы
Автор ответа:
1
нуу
мы имеем разность квадратов
a^2 - 81b^2 = (a-9b)(a+9b)
слева мы можем вынести за скобку а
a^2 -9ab = a(a-9b)
домножим первую дробь на (a+9b), а вторую на (a)
получим (a(a+9b) - 9ab)/(a(a-9b)(a+9b))
вынесем вверху а за скобку
(a(a+9b -9b)/(a/(a-9b)(a+9b)
теперь можно сократить на а, получим
а/((a-9b)(a+9b)
если я не ошибаюсь, это конечный результат, сейчас перепроверю на бумаге и отпишу в комментах
мы имеем разность квадратов
a^2 - 81b^2 = (a-9b)(a+9b)
слева мы можем вынести за скобку а
a^2 -9ab = a(a-9b)
домножим первую дробь на (a+9b), а вторую на (a)
получим (a(a+9b) - 9ab)/(a(a-9b)(a+9b))
вынесем вверху а за скобку
(a(a+9b -9b)/(a/(a-9b)(a+9b)
теперь можно сократить на а, получим
а/((a-9b)(a+9b)
если я не ошибаюсь, это конечный результат, сейчас перепроверю на бумаге и отпишу в комментах
hosefulive:
в ответах (а)/(а^2-81b^2)
это то же самое, собери (a-9b)(a+9b) назад в разность квадратов, получишь a^2 -81b^2
Автор ответа:
1
1. Первая дробь: в знаменателе выносим за скобки а, вторая дробь: раскладываем знаменатель по формуле разности квадратов:
2. Первую дробь сокращаем на а:
3. Приводим дроби к общему знаменателю, домножив первую дробь на (a+9b), приводим подобные в числителе:
4. Сворачиваем знаменатель по формуле разности квадратов:
Похожие вопросы
Предмет: Математика,
автор: romchiksedyh
Предмет: История,
автор: misteriks960
Предмет: Математика,
автор: kavitayak769
Предмет: Математика,
автор: katy200312
Предмет: Математика,
автор: мак65