Предмет: Математика,
автор: Astroonaut
Помогите пожалуйста, нужно решение и рисунок. Из трех досок 1 м,1 м и 2 м требуется изготовить желоб наибольшего объема под каким углом должны быть бока этого желоба?
Ответы
Автор ответа:
1
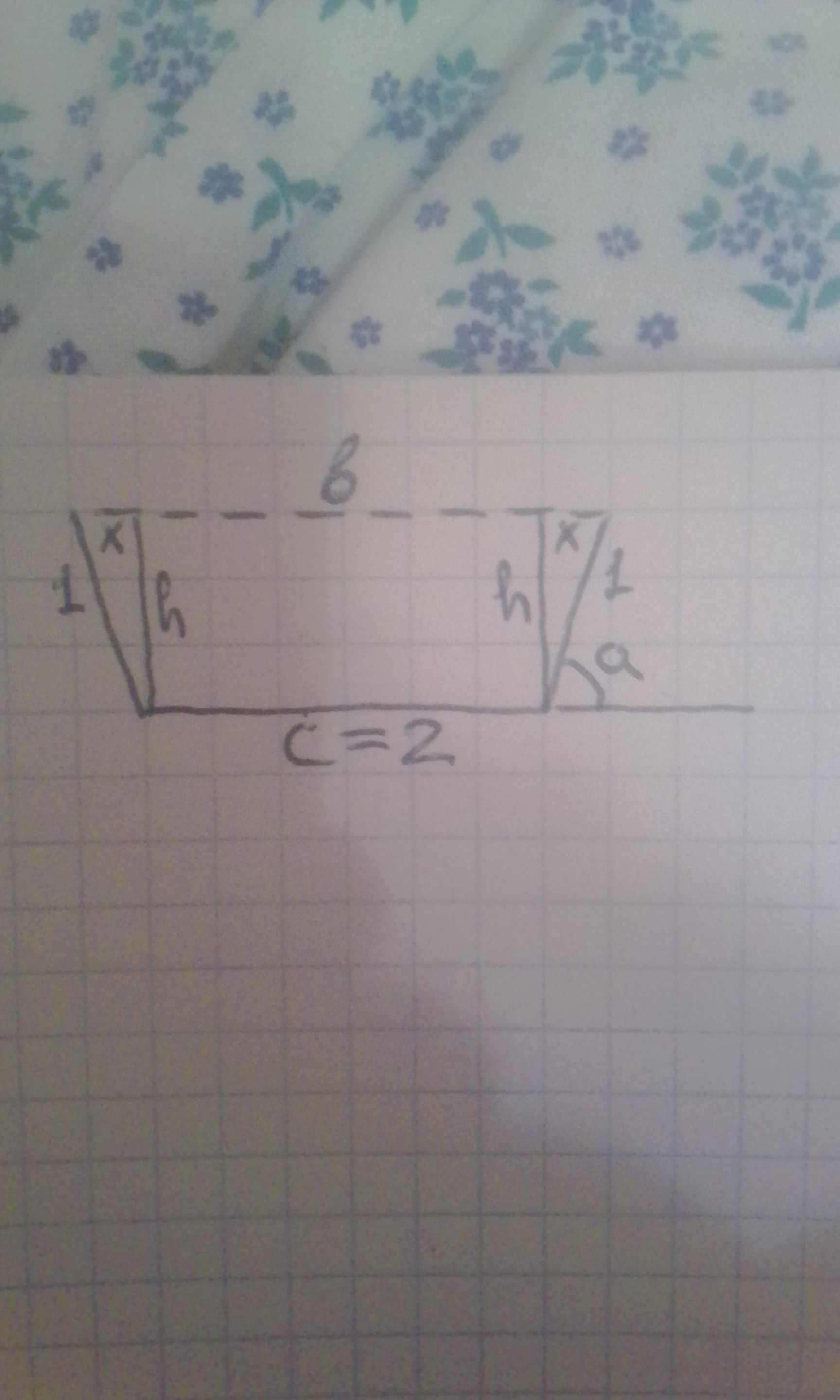
Вот рисунок я нарисовал.
Поперечное сечение желоба - это равнобочная трапеция.
Угол а наклона стенок желоба меняется от 0 до 90°.
Если угол а = 0, то площадь сечения равна 0, и объем тоже 0.
Если угол а = 90°, то h = 1, площадь S = 1*2 = 2, это прямоугольник.
Если угол а < 90°, то
h = 1*cos(90°-a) = sin a
Верхнее основание
b = c + 2x = 2 + 2*sin(90°-a) = 2 + 2cos a
Тогда площадь
S = 1/2*(b+c)*h = 1/2*(2+2cos a+2)*sin a = (2+cos a)*sin a
Площадь будет наибольшей в точке экстремума, когда S' = 0.
S' = cos a*(2+cos a) + (-sin a)*sin a = 0
2cos a + cos^2 a - sin^2 a = 0
2cos a + cos^2 a + (1-sin^2 a) - 1 = 0
2cos^2 a + 2cos a - 1 = 0
D = 2^2 - 4*2(-1) = 4+8 = 12
cos a = (-2 -√12)/4 = (-1-√3)/2 < -1 - не подходит.
cos a = (-2 + √12)/4 = (-1+√3)/2 - подходит.
Ответ: Угол a = arccos[(√3-1)/2] ~ 68,5° от горизонтали.
Поперечное сечение желоба - это равнобочная трапеция.
Угол а наклона стенок желоба меняется от 0 до 90°.
Если угол а = 0, то площадь сечения равна 0, и объем тоже 0.
Если угол а = 90°, то h = 1, площадь S = 1*2 = 2, это прямоугольник.
Если угол а < 90°, то
h = 1*cos(90°-a) = sin a
Верхнее основание
b = c + 2x = 2 + 2*sin(90°-a) = 2 + 2cos a
Тогда площадь
S = 1/2*(b+c)*h = 1/2*(2+2cos a+2)*sin a = (2+cos a)*sin a
Площадь будет наибольшей в точке экстремума, когда S' = 0.
S' = cos a*(2+cos a) + (-sin a)*sin a = 0
2cos a + cos^2 a - sin^2 a = 0
2cos a + cos^2 a + (1-sin^2 a) - 1 = 0
2cos^2 a + 2cos a - 1 = 0
D = 2^2 - 4*2(-1) = 4+8 = 12
cos a = (-2 -√12)/4 = (-1-√3)/2 < -1 - не подходит.
cos a = (-2 + √12)/4 = (-1+√3)/2 - подходит.
Ответ: Угол a = arccos[(√3-1)/2] ~ 68,5° от горизонтали.
Приложения:
Похожие вопросы
Предмет: Биология,
автор: fedorovpapa88
Предмет: Математика,
автор: bulochka123137
Предмет: Математика,
автор: madinaergali
Предмет: Информатика,
автор: alexey2307
Предмет: Математика,
автор: Адылинка10