Question

Решите пожалуйста задачу.Желательно с рисунком.Докажите что геометрическое место точек удалённых от прямой а на расстоянии h состоит из двух прямых b и c параллельных прямой а и отстоящих от неё на h.

Answer 1

Т.к. расстояние от прямой до некоторой точки — это есть перпендикуляр к этой прямой через эту точку

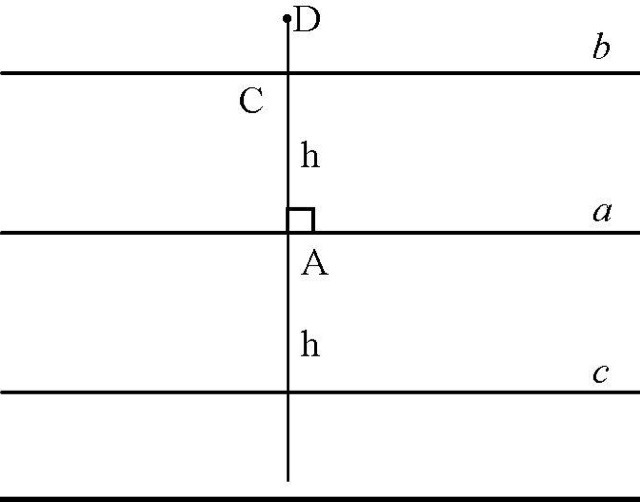
Докажем, что любая точка, удаленная от а на h лежит либо на с, либо на b.

Пусть точка D не лежит ни на b, ни на с, и расстояние от D до точки А на прямой равно h.

Тогда DA = h и AD ⊥ a.

Но СА также равно h и СА ⊥ а.

Следовательно, точки С и D либо совпадают, либо противоположны относительно прямой а.

То есть точка D лежит на прямой b или на с.