Предмет: Алгебра,
автор: artvas2000
Сделайте подробно, пожалуйста
Приложения:

Ответы
Автор ответа:
0
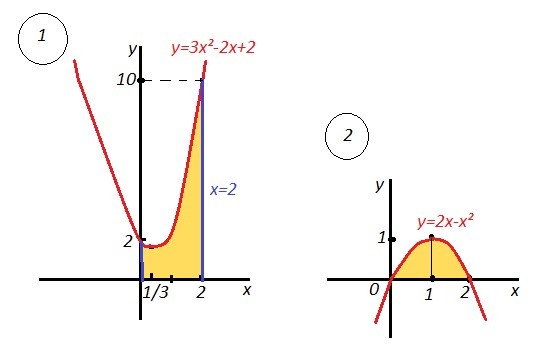
Приложения:
Похожие вопросы
Предмет: Математика,
автор: wmk2natalya
Предмет: Математика,
автор: imashevaasiyam
Предмет: Математика,
автор: ajlarakadyrova78
Предмет: Алгебра,
автор: viktoriyaorlov2