Question

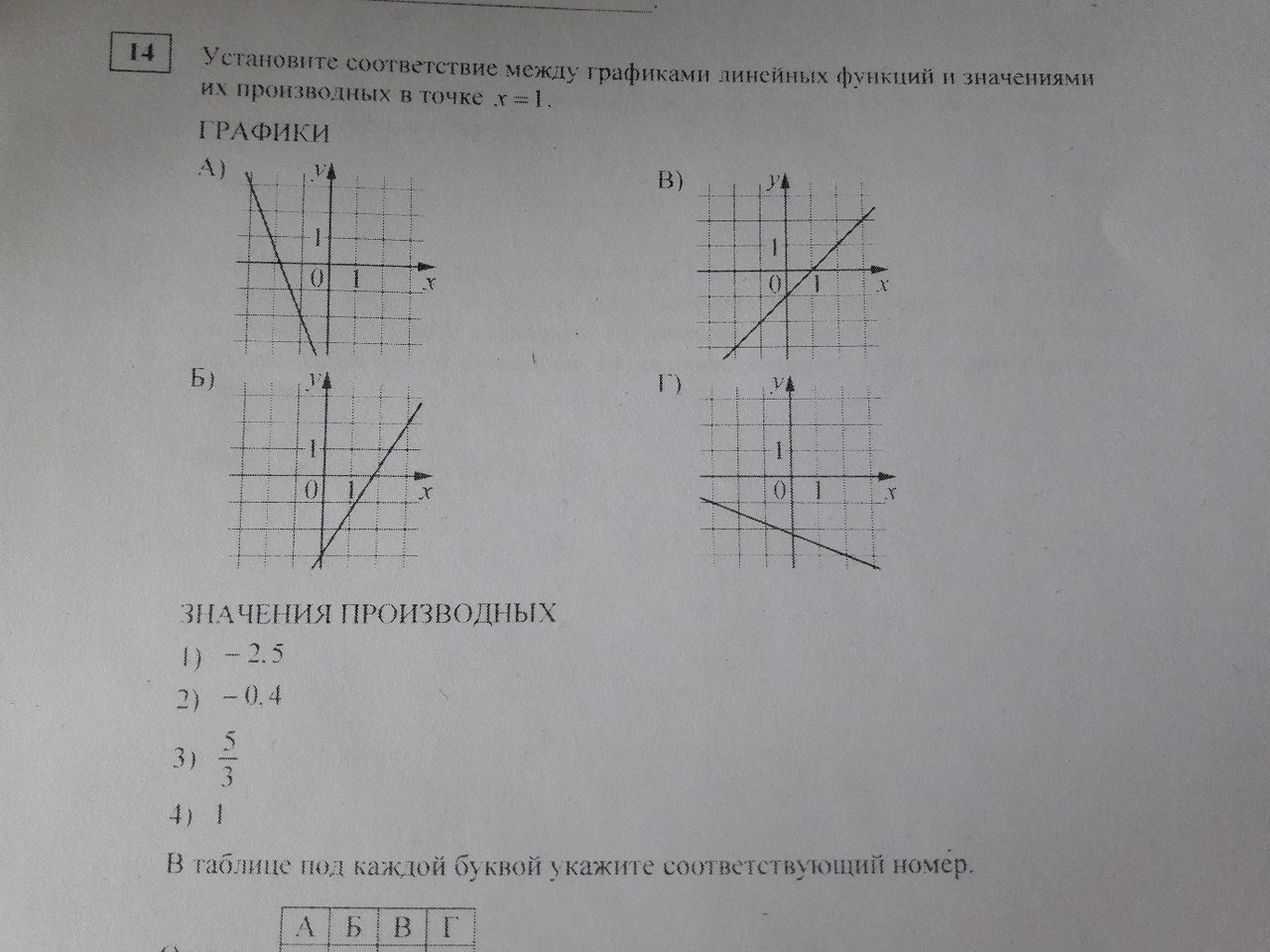
Установите соответствие между графиками линейных функций и значениями их производных в точке x=1

Answer 1

Сначала надо составить уравнения прямых .
Эти уравнения имеют вид y=kx+b , а производная y'=k . Причём производная не зависит от переменной х, и не важно, какое значение 
эта переменная будет принимать.
А)  Прямая проходит через две точки (-1,-2) и (-3,3). Подставим координаты точек в уравнение  y=kx+b и решим систему двух уравнений с двумя переменными , найдём k и b . 
y=-2,5x-4,5  ⇒  y'=-2,5
Б)  Теперь постараемся упростить выявление коэффициента k, чтобы не составлять всё уравнение.
Коэфф. k=tgα , где α - угол наклона прямой к ПОЛОЖИТЕЛЬНОМУ направлению оси ОХ. Если угол α острый, то tgα>0; если α - тупой, то tgα<0 . 
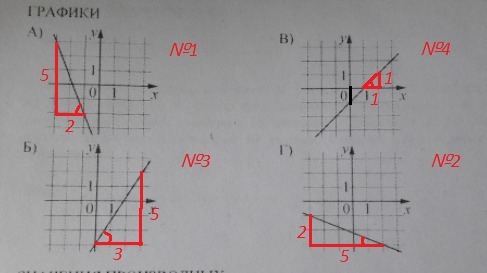
Чтобы определить tgα, достроим прямоугольные треугольники, где их гипотенузы будут лежать на указанных прямых, а катеты выберем такие, чтобы они проходили через узловые точки на прямой. Отношение противолежащего катета к прилежащему равно tgα.
  $k=y'=\frac{5}{3}$  .
В)  $y'=k=1$  .
Г)  $y'=k=-\frac{2}{5}=-0,4$  .

Ответ:  А - 1  ,  Б - 3 , В - 4 , Г - 2 .