Предмет: Алгебра,
автор: nikulina2018
Решить дробно-рациональное уравнение
Приложения:
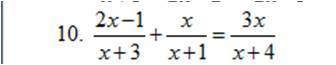
Ответы
Автор ответа:
1
вроде так ответ решений нет
Приложения:

nikulina2018:
Спасибо большое!сейчас просмотрю.Я три раза решала и три раза по разному получилось)))
незачто
Автор ответа:
1
итак, наше уравнение эквивалентно данной системе:
решим первое уравнение системы, а затем исключим из ответа ложные корни, если таковые будут
следовательно,
ОТВЕТ:
Класс!спасибо!ни за что бы не догадалась..
Похожие вопросы
Предмет: Математика,
автор: fotoshko786
Предмет: Обществознание,
автор: zarembaulia555
Предмет: Английский язык,
автор: polinanovikova523
Предмет: Математика,
автор: ezro1
Предмет: Математика,
автор: Эльза55142