Question

Пожалуйста ребята очень надо ,плиз))9 класс

Answer 1

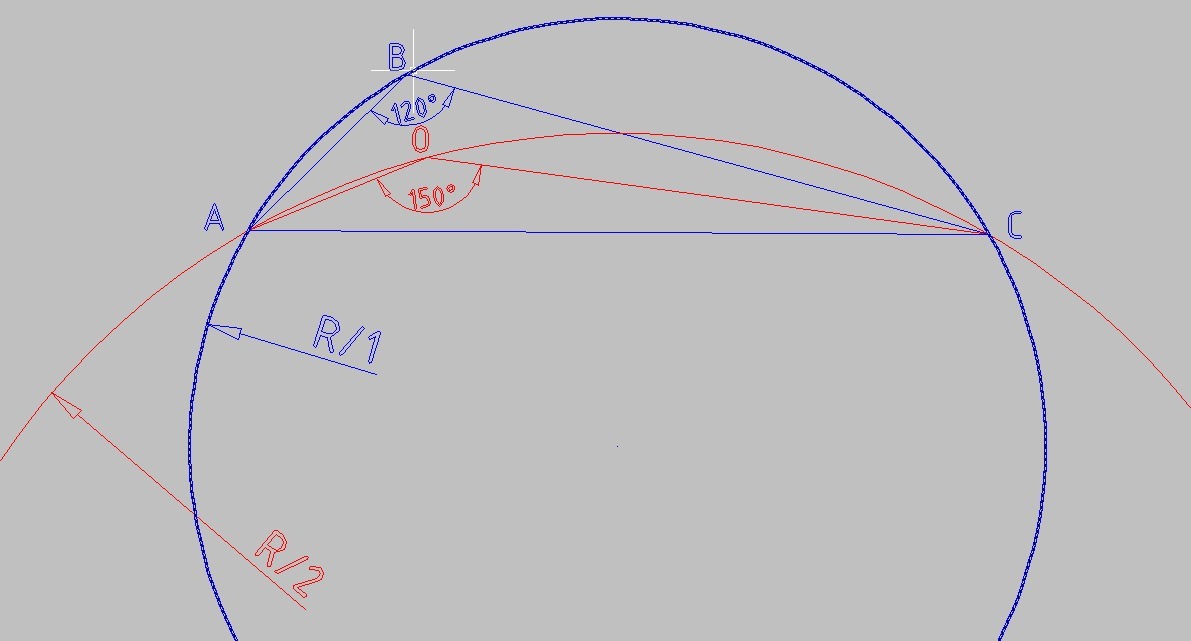
По теореме синусов для исходной окружности
2R₁ = АС/sin(∠ABC)
2R₁ = АС/sin(120°)
2R₁ = АС/(√3/2)
R₁ = АС/√3
АС = R₁√3 см
--- 
В исходном треугольнике сумма двух углов
∠ВАС + ∠ВСА = 180 - 120 = 60°
В дочернем треугольнике каждый из углов этих углов станет в два раза меньше
∠ОАС = ∠ВАС/2
∠ОСА = ∠ВСА/2
∠ОАС + ∠ОСА = ∠ВСА/2 + ∠ВАС/2 = (∠ВСА + ∠ВАС)/2 = 60/2 = 30°
∠АОС = 180 - 30 = 150°
И по теореме синусов для нового треугольника
2R₂ = АС/sin(∠AОC)
2R₂ = АС/sin(150°)
2R₂ = АС/(1/2)
R₂ = АС
R₂ = R₁√3
R₂ = 8√3 см