Question

В треугольнике одна из сторон равна 30 см. Другая сторона точкой касания вписанной окружности делится на отрезки длиной 14 и 24 см считая от конца неизвестной стороны. Найти радиус вписанной окружности. Пожалуйста дайте еще и рисунок к решению.

Answer 1

Решение на фото//////////////

Answer 2

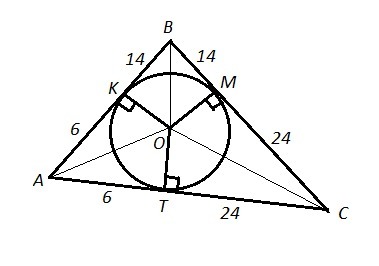
ΔАВС:  АС=30 см , точки касания вписанной окружности сторон треугольника - М, Т, К.
ВМ=14 см , СМ=24 см .  ⇒  ВС=ВМ+МС=14+24=38 (см).
По теореме : отрезки касательных, проведённых из одной точки к окружности, равны  ⇒  ВМ=ВК=14 , СМ=СТ=24 , АК=АТ.
АС=АТ+ТС  ,  30=АТ+24  ,  АТ=30-24=6   ⇒  АК=АТ=6  .
АВ=АК+ВК=6+14=20 .
Радиус вписанной окружности находим из формулы для площади треугольника:  S=pr , r - радиус впис. окр.,  р - полупериметр.
S можно ещё найти из формулы Герона:

  $S=\sqrt{p(p-a)(p-b)(p-c)} \; ,\\\\p=\frac{1}{2}\cdot (30+38+20)=44\; ,\\\\p-a=44-38=6\; ,\; p-b=44-30=14\; ,\; \; p-c=44-20=24\\\\S=\sqrt{44\cdot 6\cdot 14\cdot 24}=\sqrt{(4\cdot 11)\cdot 6\cdot (2\cdot 7)\cdot (4\cdot 6)}=\\=4\cdot 6\cdot \sqrt{11\cdot 2\cdot 7}=24\cdot \sqrt{154}\\\\S=pr\; \; \to \; \; r=\frac{S}{p}=\frac{24\cdot \sqrt{154}}{44}= \frac{6\cdot \sqrt{154}}{11}$