Question

94 балла!
Основанием призмы АВСDА1В1С1D1 является ромб ABCD, в котором острый угол А равен альфа. Плоскость гамма, проходящая через одну из вершин нижнего основания и меньшую диагональ нижнего основания призмы, образует с плоскостью основания угол бета. Высота призмы равна h.

1) Постройте сечение. (рисунок в решении — обязательно!)
2) Определитель площадь этого сечения.

Answer 1

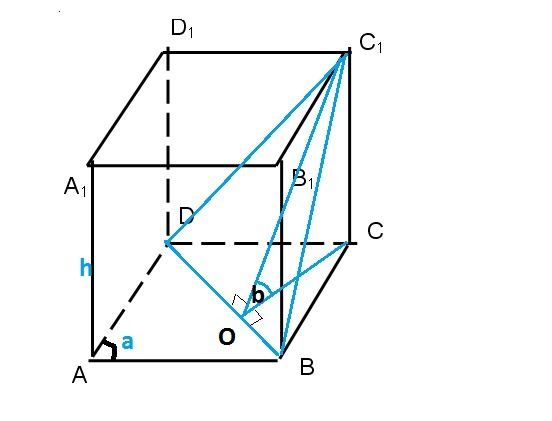
Сечение DBC1-равнобедренный Δ
S(DBC1)=OB*OC1
OC1-высота в ΔDBC1
OC-высота в равнобедренном ΔDBC(DC и ВС-стороны ромба)
ΔOCC1-прямоугольный
OC1=CC1/sinb=h/sinb
tgb=CC1/OC=h/OC; OC=h/tgb
ΔCOB-прямоугольный
tg(a/2)=OB/OC; OB=OC*tg(a/2)=h*tg(a/2)/tgb
S(DBC1)=OB*OC1=(h*tg(a/2)/tgb)*(h/sinb)=h^2*tg(a/2)/(sinb*tgb)=
=h^2*tg(a/2)*ctgb/sinb