Предмет: Геометрия,
автор: terminatorsasha
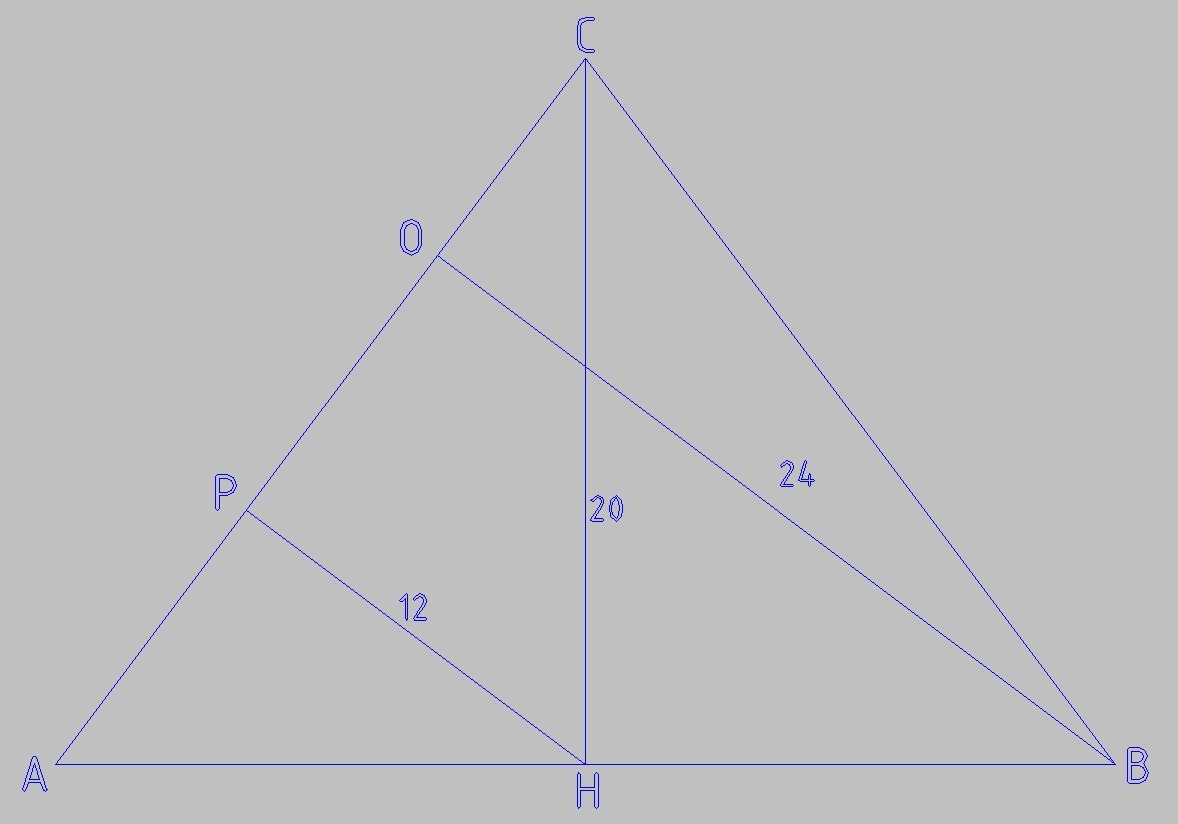
Висота рівнобедреного трикутника, проведена до основи, дорівнює 20см, а висота, проведена до бічної сторони – 24 см. Знайти площу цього трикутника, якщо його бічна сторона відноситься до основи як 5:6.
Ответы
Автор ответа:
13
Рассмотрим ΔАСН, являющийся половиной исходного. Площадь его в два раза меньше
S(ACH) = 1/2*AC*РН
S(АВС) = 1/2*АС*ОВ
ОВ = 24 по условию, значит, РН = 12
В прямоугольном ΔСРН по теореме Пифагора
СР² + РН² = СН²
СР² + 12² = 20²
СР² + 144 = 400
СР² = 256
СР = 16
ΔСРН и ΔАСН подобны - один угол общий, один угол прямой
СР/СН = СН/СА
16/20 = 20/СА
СА = 400/16 = 25 см
И площадь ΔАВС
S(АВС) = 1/2*АС*ОВ = 1/2*25*24 = 300 см²
S(ACH) = 1/2*AC*РН
S(АВС) = 1/2*АС*ОВ
ОВ = 24 по условию, значит, РН = 12
В прямоугольном ΔСРН по теореме Пифагора
СР² + РН² = СН²
СР² + 12² = 20²
СР² + 144 = 400
СР² = 256
СР = 16
ΔСРН и ΔАСН подобны - один угол общий, один угол прямой
СР/СН = СН/СА
16/20 = 20/СА
СА = 400/16 = 25 см
И площадь ΔАВС
S(АВС) = 1/2*АС*ОВ = 1/2*25*24 = 300 см²
Приложения:
Похожие вопросы
Предмет: Химия,
автор: evelinalobastova036
Предмет: Алгебра,
автор: Ybitsa22866613337
Предмет: Химия,
автор: Lelinda
Предмет: Математика,
автор: elyakot00