Предмет: Алгебра,
автор: technodance
77.
Вычислите f'(\frac{\pi}{9} , если f(x)= lncos3x.
technodance:
Пи\9
какие там ответы есть?
Ответы
Автор ответа:
1
Решение во вложении. Успехов в алгебре!
Приложения:
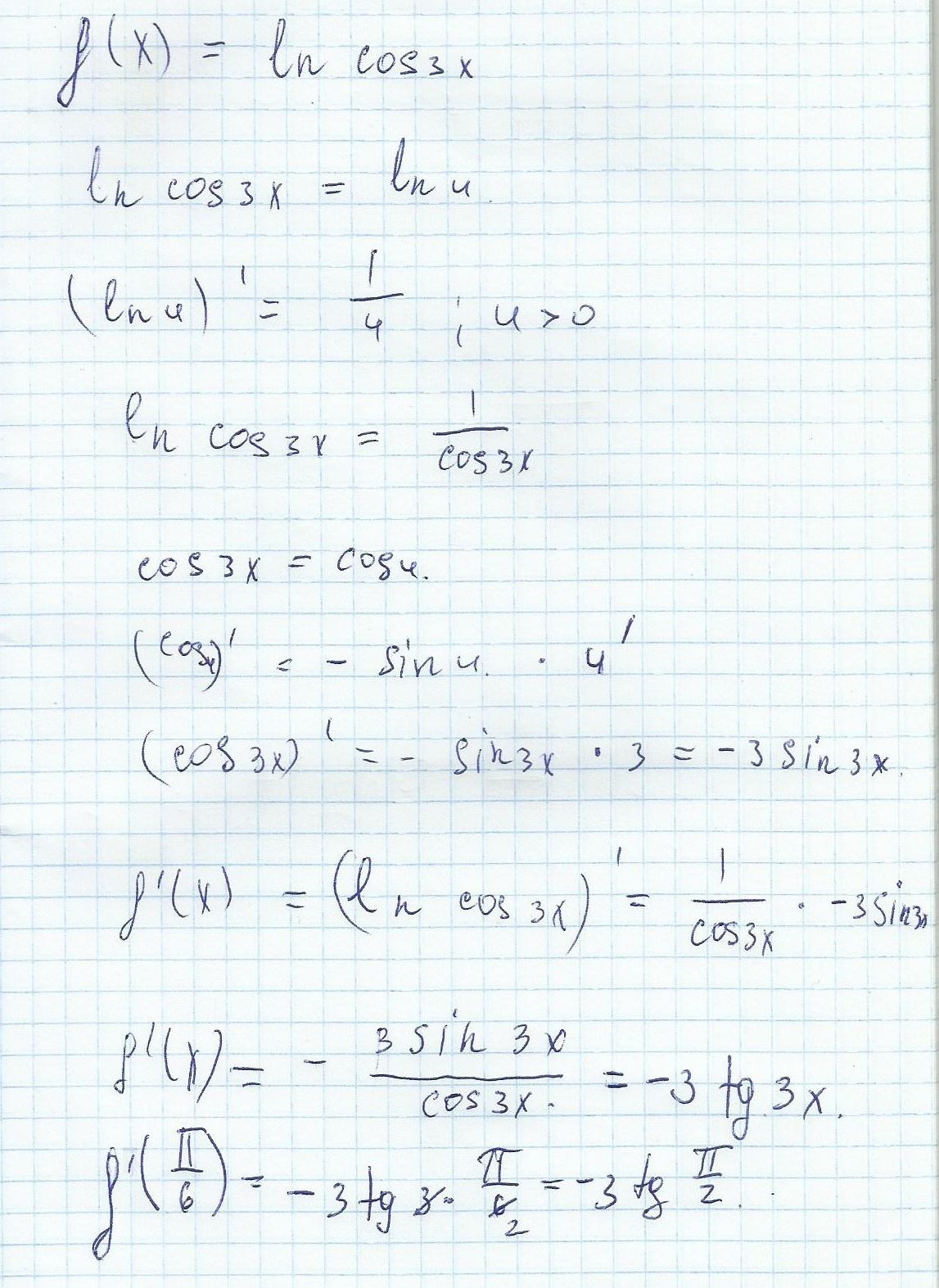
Автор ответа:
0
найти  , если
, если 


Похожие вопросы
Предмет: Физика,
автор: raufov4477
Предмет: Математика,
автор: Аноним
Предмет: Английский язык,
автор: leonidcherkov2000
Предмет: Математика,
автор: dfkthrf2711
Предмет: Математика,
автор: регоро