Question

Две взаимно перпендикулярные прямые имеют общую точку О. Окружности, радиусов равны 3 и 4, касаются обеих прямых. Чему может быть равно расстояние между центрами этих окружностей? (Рассмотрите все возможные случаи.)

Answer 1

Всего возможны 4 варианта, но два дают равное расстояние между центрами окружностей, итого - три разных расстояния
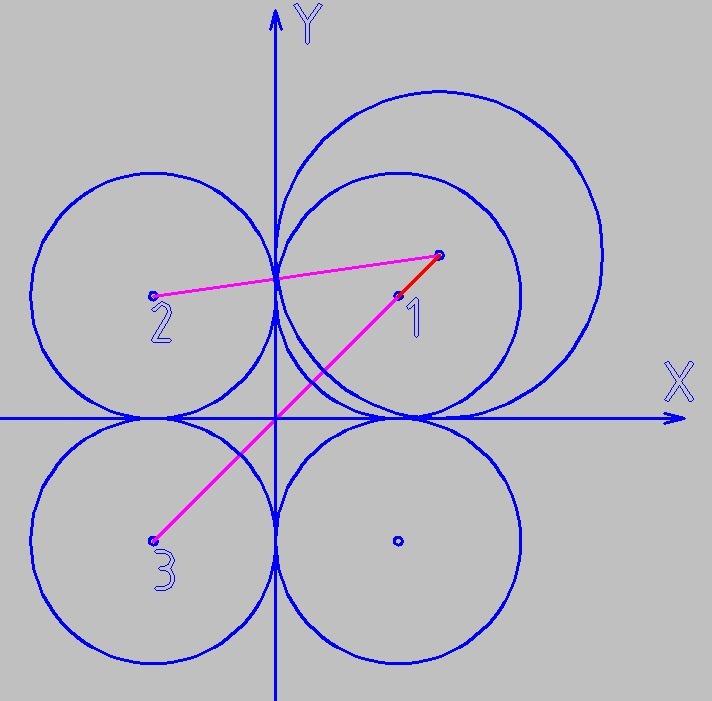
Координаты центра большой окружности (4;4)
1. Координаты центра меньшей окружности (3;3)
R² = (4-3)² + (4-3)² = 1² + 1² = 2
R = √2
2. Координаты центра меньшей окружности (-3;3)
R² = (4+3)² + (4-3)² = 7² + 1² = 50
R = 5√2
3. Координаты центра меньшей окружности (-3;-3)
R² = (4+3)² + (4+3)² = 7² + 7² = 98
R = 7√2