Question

Равнобедренный треугольник АВС вписан в окружность основание треугольника АС равно радиусу окружности найдите велечины дуг АС АВ ВС

Answer 1

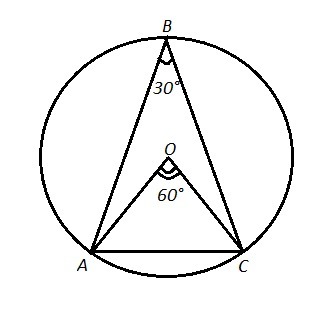
ΔАВС - равнобедренный ,  АВ=ВС.
Так как АС=R=ОА=ОС, R - радиус описанной окружности, то ΔАОС - равносторонний, значит все его углы = 60°.
Центральный ∠АОС=60°  ⇒  вписанный ∠АВС, опирающийся на ту же дугу АС , равен 60°:2=30°. 
Cама дуга АС равна 60°, т.к. центральный угол АОС в 60°опирается на эту дугу.
При основании равнобедренного Δ углы равны  ⇒
∠ВАС=∠ВСА=(180°-30°):2=150°:2=75° - это вписанные углы.
Тогда дуги, на которые эти углы опираются,  равны 75°*2=150°  ⇒
дуга ВС = дуге АВ =150°.