Question

помогите!
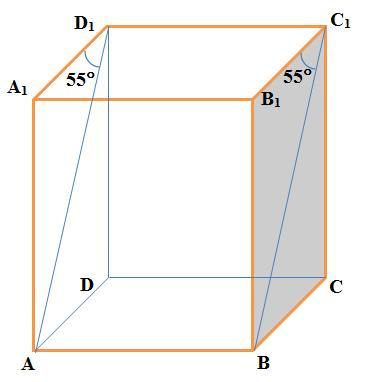
В прямоугольном параллелепипеде ABCDA1B1C1D1 угол BC1B1=55, найдите угол между прямыми C1B и AA1

Answer 1

Ответ:

Угол между прямыми C₁B и AA₁ равен 35°

Объяснение:

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся (не лежат в одной плоскости).  

В задаче C₁B и AA₁ являются скрещивающимися прямыми (см. рисунок). Углом между двумя скрещивающимися прямыми называют угол между двумя пересекающимися прямыми, соответственно, параллельными данным скрещивающимся прямым.

В силу этого, так как C₁B || D₁A, то угол между прямыми C₁B и AA₁ равен углу между прямыми D₁A и AA₁, то есть ∠A₁AD₁. В треугольнике ΔAA₁D₁:

∠AD₁A₁+∠D₁A₁A+∠A₁AD₁=180°.

Тогда, так как ∠AA₁D₁=90° и ∠AD₁A₁=55°, то ∠A₁AD₁=180°–90°–55°=35°.