Question

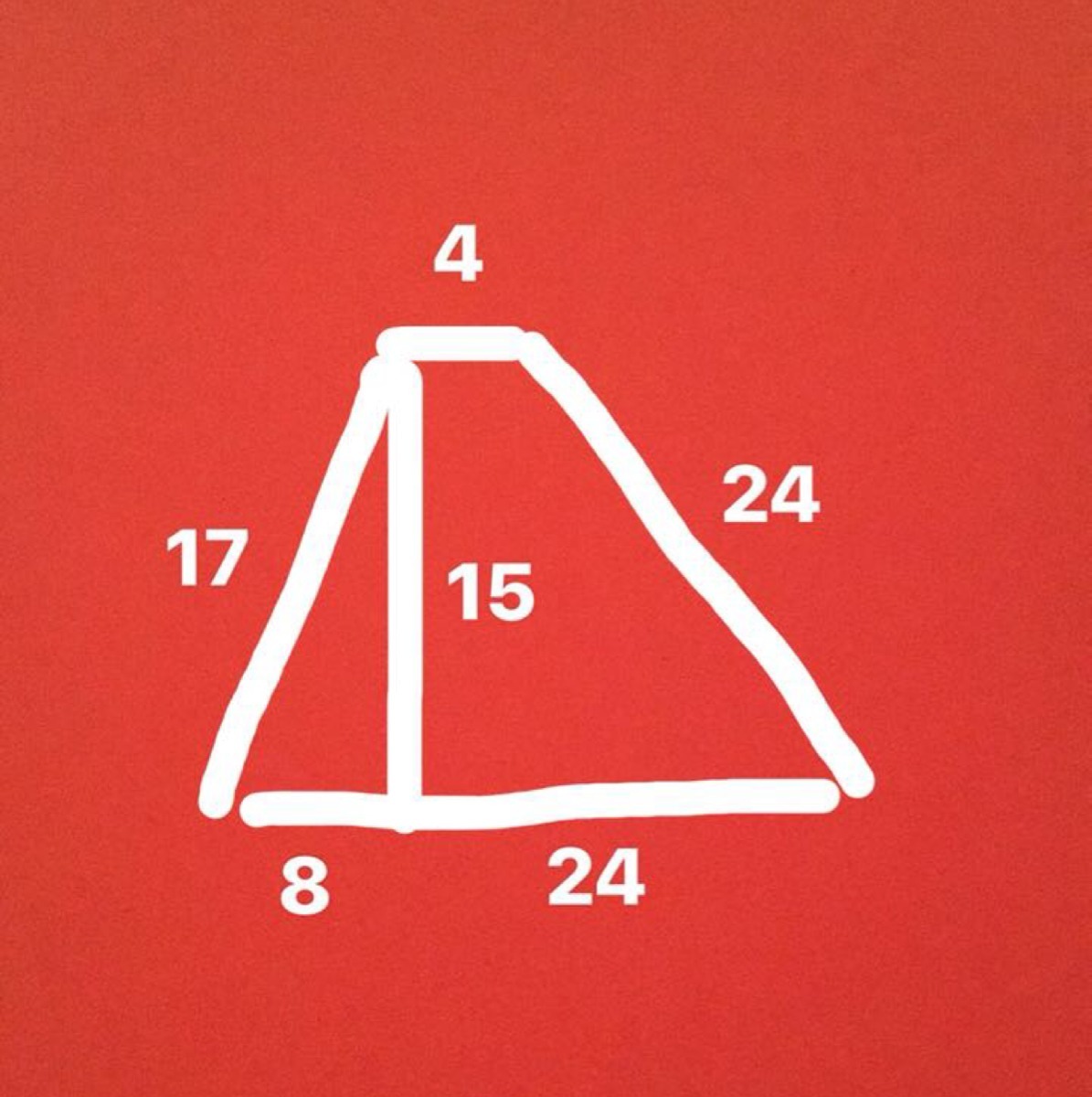
Найдите площадь трапеции, изображённой на рисунке
8 класс

Answer 1

В условии ошибка: трапеции с такими сторонами быть не может. Правая сторона должна равняться 25 см, чтобы все остальные числа оставались такими.

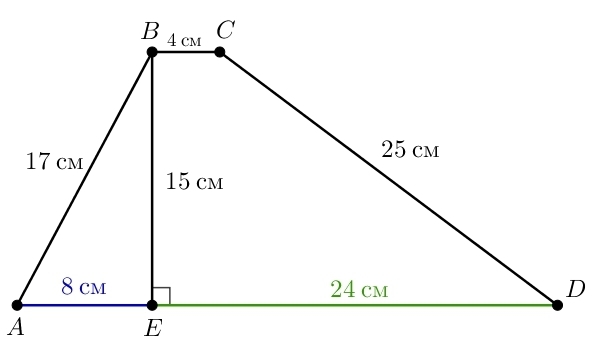
Площадь трапеции равна полусумме сторон, умноженной на высоту (обозначения см на рисунке):
$S=\frac{BC+AD}{2}\cdot BE= \frac{4+(24+8)}{2} \cdot 15= \frac{36}{2} \cdot 15=18 \cdot 15=270$ см².в

Ответ: 270 см² при условии, что правая боковая сторона равна 25 см.

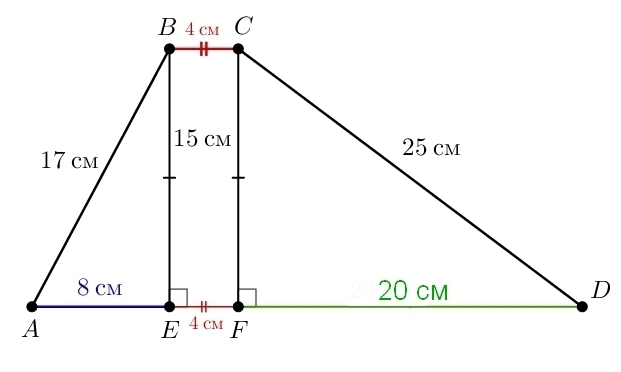
P. S. Для доказательства того, что сторона должна равняться именно 25 см, опустим на сторону AD перпендикуляр CF (см. второй рисунок). BE=CF как перпендикуляры, BC=EF как противоположные стороны прямоугольника. Следовательно, FD=24–4=20 см. Применим теорему Пифагора к треугольнику CDF:
$FD^2+CF^2=CD^2\\CD^2=20^2+15^2=400+225=625\\CD=\sqrt{625}=25$

что и требовалось доказать.