Question

Срочно!!!!!!!!!!Помогите решить!
Через диагональ нижнего основания правильной четырёхугольной призмы параллельно диагонали призмы проведено сечение.Диагональ основания призмы равна 3 корня из 3,а площадь сечения 9 корней из 2.Найдите диагональ призмы
Ответ:4 корня из 6

Answer 1

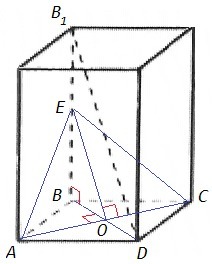
В основании правильной четырехугольной призмы - квадрат. Диагонали квадрата перпендикулярны, точкой пересечения делятся пополам.

O - точка пересечения диагоналей основания ABCD.
Сечение AEC проходит через AC, пересекает ребро BB1 в точке E, EO || B1D.

EO⊥AC по теореме о трех перпендикулярах (BB1⊥BD, BO⊥AC)
S(AEC)= AC*EO/2 <=> 9√2= EO*3√3/2 <=> EO= 6√2/√3 =2√6

△BB1D~△BEO (B1D || EO), k=BD/BO=2
B1D= EO*2 =4√6