Question

ДАЮ 40 БАЛЛОВ
Отрезок АВ является диаметром окружности центр которой - точка О.Точка С лежит на окружности, АО=АС. Вычислите площадь треугольника АВС и расстояние от точки С до прямой АВ, если АВ = 12см.

Answer 1

AO=1/2*AB=6см
С лежит на окружности,значит угол С равен 90гр (вписанный,опирается на дугу 180гр)
BC=√AB²-AC²=√144-36=√108=6√3см
S=1/2*AC*BC=1/2*6*6√3=18√3см²

Answer 2

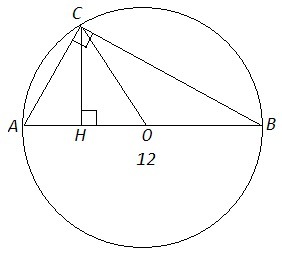
△ACO - равносторонний (AО=CO, радиусы). Высота в равностороннем треугольнике равна a√3/2 (a - сторона).
AO=AB/2 =6
CH=AO*√3/2 =3√3 (см)
S(ABC)=AB*CH/2 =12*3√3/2 =18√3 (см^2)

ИЛИ

Вписанный угол ∠ACB - прямой, так как опирается на диаметр. Катет AC равен половине диаметра, то есть половине гипотенузы. В треугольнике ABC стороны относятся как 1 : √3 : 2
AC=6, BC=6√3
S=6*6√3/2=18√3 (см^2)

△ACH подобен △ABC по двум углам (прямоугольные с общим углом), k=AC/AB=1/2
CH=BC*k=3√3 (см)