Question

Площадь прямоугольной трапеции равна 144 кв. см. А её высота 9 см. Найти все стороны трапеции, если одно основание больше другого на 12 см.

Answer 1

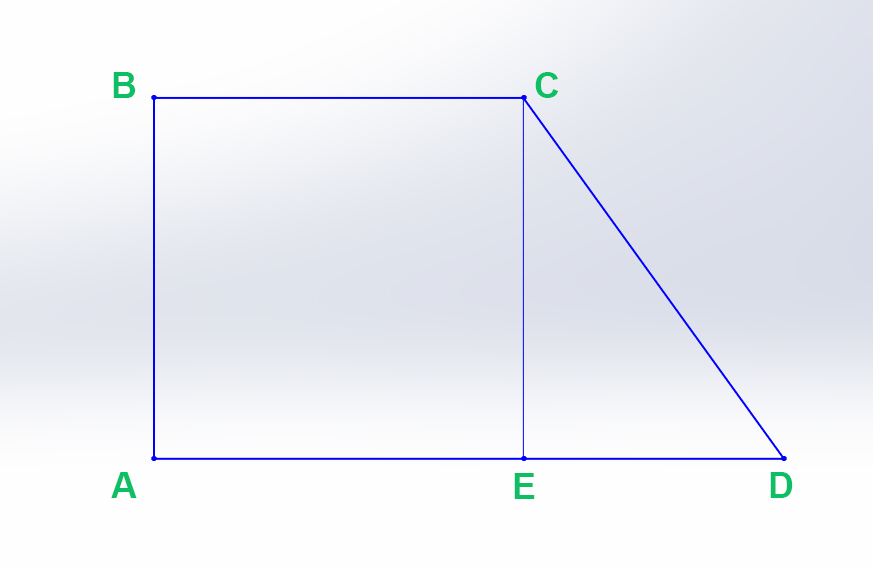
Пусть нижнее основание AD=x, тогда по условию верхнее основание будет BC=x-12
$S= \frac{AD+BC}{2}*AB$ ⇒ $144= \frac{x+x-12}{2}*9$ ⇒ 2x=44 ⇒ x=22 см (AD)
x-12=22-12=10 см  (BC)
ED=12 см (по условию или AD-BC=22-10=12)
$CD^{2}=AB^{2}+ED^{2}=9^{2}+12^{2}= 225$ ⇒ CD=√225=15 см