Question

Помогите, очень нужно!! Вычислить площадь фигуры ограниченной линиями у=2 у=(х-2)^2+1

Answer 1

у = 2 
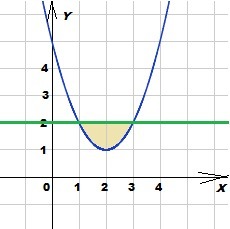
График функции : прямая линия, параллельная оси ОХ, проходящая через точку (0; 2)

у = (х - 2)² + 1
График функции : квадратичная парабола с вершиной в точке (2;1),
ветви направлены вверх.

Точки пересечения графиков:
(x - 2)² + 1 = 2
x² - 4x + 4 + 1 - 2 = 0
x² - 4x + 3 = 0
Корни уравнения по теореме Виета    x₁ = 3; x₂ = 1

Площадь снизу ограничена параболой g(x) = (х - 2)²+1,
сверху ограничена прямой f(x) = 2.
Обе функции непрерывны.
Область интегрирования  x ∈ [1; 3]
$S = \int\limits^3_1 {(f(x) - g(x))} \, dx = \int\limits^3_1 {(2 - ((x-2)^2 + 1))} \, dx = \\ \\ = \int\limits^3_1 {(2 - (x^2-4x+5))} \, dx = \int\limits^3_1 {(-x^2+4x-3)} \, dx = \\ \\= - \frac{x^3}{3} + \frac{4x^2}{2} -3x|^3_1= \\ \\ =(- \frac{3^3}{3}+2*3^2-3*3 )-(- \frac{1}{3}+2-3 )=1 \frac{1}{3}$

Ответ: $S = 1 \frac{1}{3}$