Question

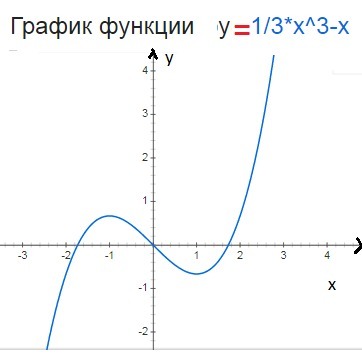
Постройте график функции f(x) = 1/3 x^3 - x

Answer 1

найдем экстремумы
f'(x)=x²-1
f'(x)=0
x²-1=0
x²=1
x1=1
x2=-1
рассмотрим знаки производной на интервалах

1) х∈(-∞;-1) возьмем какое либо число из этого интервала и подставим в производную например х=-2 f'=4-1=3 >0 значит на этом интервале функция возрастает. также сделаем на других интервалах
2) х∈(-1;1) x=0 f'=0-1=-1<0 f убывает
3) х∈(1;+∞) x=2 f'=4-1=3 >0 f возрастает
значит в точке -1 максимум 
в точке х=1 минимум

f(-1)=-1/3+1=2/3
f(1)=1/3-1=-2/3
точка пересечения с осью ОХ х=0 у=0