Question

Найдите радиус окружности,вписанной в прямоугольный треугольник,если биссектриса острого угла делит его противолежащий катет на отрезки длиной 8 см и 10 см.
Заранее благодарю!

Answer 1

Биссектриса делит противоположную сторону пропорционально прилежащим сторонам
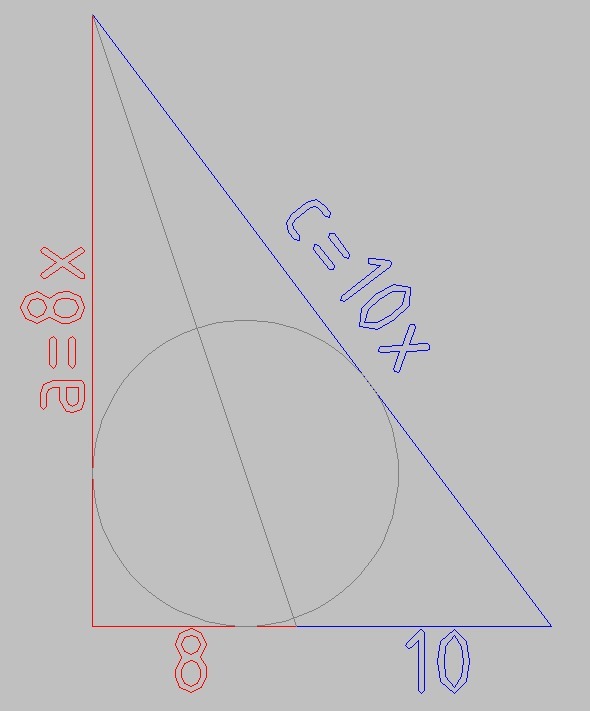
а = 8x см
b = 8+10 = 18 см
c = 10x см
По теореме Пифагора
a² + b² = c²
(8x)² + 18² = (10x)²
64x² + 324 = 100x²
36x² = 324
x² = 9
x = 3 см
Стороны треугольника 
а = 8x = 24 см
c = 10x = 30 см
Площадь через катеты
S = 1/2*a*b = 1/2*24*18 = 24*9 = 216 см²
Полупериметр
p = 1/2(a + b + c) =1/2(24 + 18 + 30) = 12 + 9 + 15 = 36 см
Площадь через полупериметр и радиус вписанной окружности
S = rp
216 = r*36
r = 6 см