Предмет: Математика,
автор: stebone
Прошу подробного решения сего неравенства:
Приложения:
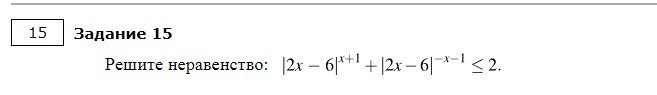
mmb1:
сие неравенство решаем аки заменой !2x-6!^(x+1)=t и получается нижеследуюшее t+ 1/t <=2 t=1 И будьте любезны продолжить сами. Вельми понеже
Благодарю)
Ответы
Автор ответа:
1
|2x-6|^(x+1) + |2x-6|^(-x-1)<=2
одз |2x-6|<>0 x<>3
|2x-6|^(x+1)=t t>=0
t + 1/t <=2
t^2-2t+1<=0
(t-1)^2<=0 выражение слева может быть только равно 0, так как слева стоит величина большая или равная 0, а справа 0
t=1
|2x-6|^(x+1)=1
пролоргарифмируем
(x+1)lg !2x-6! = 0
x=-1
2x-6=1
x=7/2
2x-6=-1
x=5/2
ответ -1 5/2 7/2
одз |2x-6|<>0 x<>3
|2x-6|^(x+1)=t t>=0
t + 1/t <=2
t^2-2t+1<=0
(t-1)^2<=0 выражение слева может быть только равно 0, так как слева стоит величина большая или равная 0, а справа 0
t=1
|2x-6|^(x+1)=1
пролоргарифмируем
(x+1)lg !2x-6! = 0
x=-1
2x-6=1
x=7/2
2x-6=-1
x=5/2
ответ -1 5/2 7/2
Это же неравенство а не уравнение здесь должны быть указаны промежутка
о как !
если Вы мне найдете промежутки, то я вам спасибо скажу
неравенство t+1/t<2 сколько решений имеет a t+1/t<=2 ?
если Вы мне найдете промежутки, то я вам спасибо скажу
неравенство t+1/t<2 сколько решений имеет a t+1/t<=2 ?
будет
1...........
А если логарифмировать то нужно прибавлять lg или log
а у меня нет lg? 7-я строка снизу
Похожие вопросы
Предмет: Геометрия,
автор: michaelUrban
Предмет: Геометрия,
автор: nastyaabdraimova
Предмет: Физика,
автор: broken11bro
Предмет: Математика,
автор: Аноним