Предмет: Геометрия,
автор: Vlada1N
В равнобедренном треугольнике боковая сторона 10см, а биссектриса, провеленная к основанию 8см.Найдите радиус окружности, вписанной в этот треугольник и радиус окружности, описанной около этого треугольника. Можно с чертежем? Спасибо
Ответы
Автор ответа:
4
Смртри на фото там решение и рисунок
Приложения:
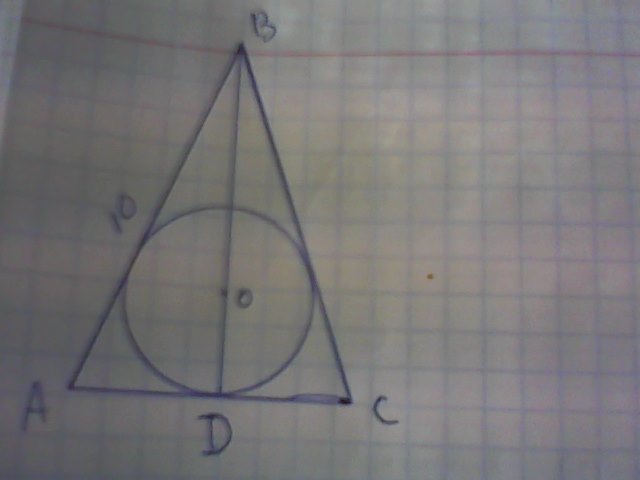

Автор ответа:
0
найдем площадь треугольника. В равнобедренном тр-ке биссектриса, проведенная к основанию, является также медианой и высотой. Найдем половину основания по теореме Пифагора.
10^2-8^2=100-64=36. Значит половина основания равна √36=6 см, а основание 12 см.
Площадь тр-ка равна половине произведения стороны на высоту, проведенную к этой стороне
S=½*12*8=48 см кв.
Радиусы описанной (R) и вписанной (r) окружностей найдем из формул этих радиусов
R=abc/4S=10*10*12/4*48=1200/192=6,25 см
r=2S/(a+b+c)=2*48/(10+10+12)=96/32=3 см
10^2-8^2=100-64=36. Значит половина основания равна √36=6 см, а основание 12 см.
Площадь тр-ка равна половине произведения стороны на высоту, проведенную к этой стороне
S=½*12*8=48 см кв.
Радиусы описанной (R) и вписанной (r) окружностей найдем из формул этих радиусов
R=abc/4S=10*10*12/4*48=1200/192=6,25 см
r=2S/(a+b+c)=2*48/(10+10+12)=96/32=3 см
Похожие вопросы
Предмет: Українська мова,
автор: dimon4ik2701
Предмет: Алгебра,
автор: kaverthlina976
Предмет: Українська література,
автор: crinder
Предмет: Биология,
автор: kdickareva
Предмет: Математика,
автор: амина156