Question

В равностороннем треугольнике ABC проведена биссектриса AD.
Расстояние от точки D до прямой AB равно 6 см. Найдите AD

Answer 1

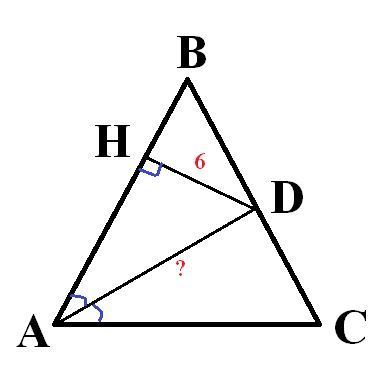
Чертеж - во вложении.
Пусть ДН - расстояние от Д до АВ. Тогда ДН⊥АВ. Значит, Δ АДН - прямоугольный.
Т.к. АД - биссектриса равностороннего треугольника, то ∠ВАД=∠САД=30°.
В прямоугольном ΔАНД ∠НАД=30°, значит, противолежащий ему катет НД в 2 раза меньше гипотенузы АД. Т.е. АД = 2·6 = 12 см.
Ответ: 12 см.