Question

постройте график функции:
$y = \frac{ ({x}^{2} + 2.25)(x + 1) }{ - 1 - x}$
Определите, при каких значениях k прямая y=kx имеет с графиком ровно одну общую точку.
Заранее большое спасибо)))

Answer 1

Упростим данную функцию:
                                                   $y = \dfrac{ ({x}^{2} + 2.25)(x + 1) }{ - 1 - x} =- \dfrac{ ({x}^{2} + 2.25)(x + 1) }{x+1} =-x^2-2.25$            (*)
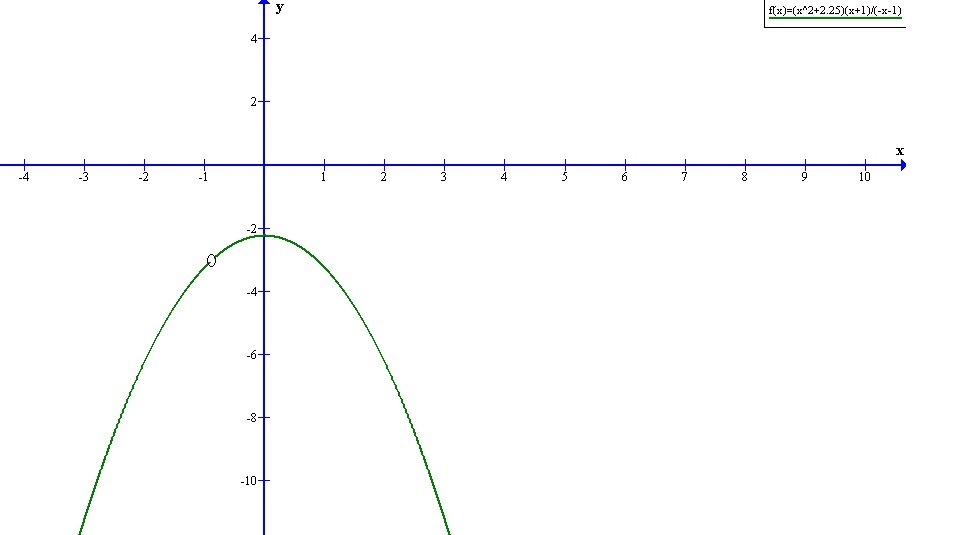
Графиком функции является парабола, ветви которого направлены вниз(так как а=-1<0) и (0;-2.25) - координаты вершины параболы.

Область определения данной функции: $-1-x\ne 0~~\Rightarrow~~~ x\ne-1$

Подставляя y=kx в упрощенную функцию, имеем
   $kx=-x^2-2.25\\ x^2+kx+2.25=0$
Для установления корней квадратного уравнения достаточно найти его дискриминант.
$D=b^2-4ac=k^2-4\cdot1\cdot2.25=k^2-9$
Квадратное уравнение имеет один действительный корень, если D=0
$k^2-9=0\\ k=\pm 3$

То есть, при k=±3 графики функций будут пересекаться в одной точке. Но это еще не все, если y=kx будет проходить в проколотую точку, то графики тоже будут пересекаться в одной точке.

Найдем значение функции (*) в точке x=-1, получаем 
    $y(-1)=-(-1)^2-2.25=-1-2.25=-3.25$

То есть, при  $k=3.25$ графики функций будут пересекаться в одной точке



Ответ: при k=±3 и k=3.25