Предмет: Математика,
автор: macsibodrov
Ctg^2 x-ctg^2 y= (cos^2 x-cos^2 y)/(sin^2 x-sin^2 y) Доказать тождество
Приложения:
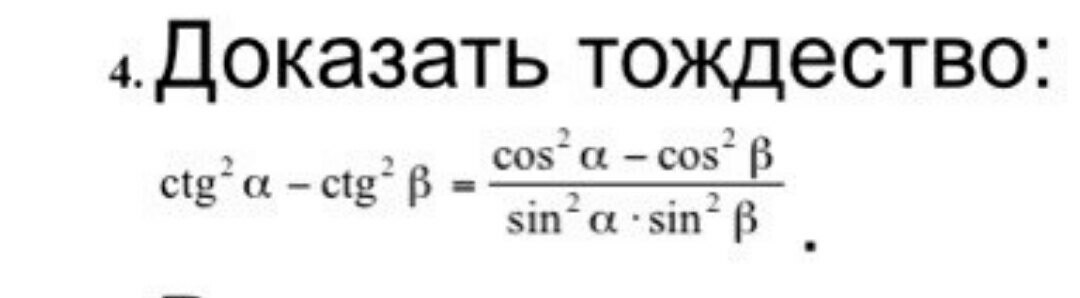
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Математика,
автор: nutaanna49
Предмет: Литература,
автор: nastya524352
Предмет: Физика,
автор: alexgrib1806
Предмет: Математика,
автор: Amikolya111
Предмет: Математика,
автор: takaaka37