Question

Решите с дано и с объяснениями:

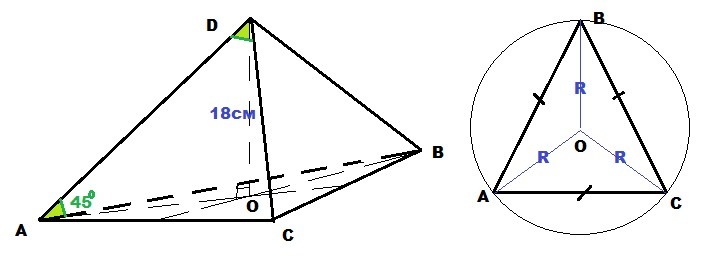
3.В правильной треугольной пирамиде боковое ребро с плоскостью основания образует угол 45°. Высота пирамиды равна 18 см. Найдите площадь основания пирамиды.

Answer 1

Дано: DABC - правильная пирамида - AB=BC=AC; DO = 18 см
∠DAO = 45°
Найти: S₀ -?

Высота правильной пирамиды опускается в центр вписанной/описанной окружности ⇒
OA = OB = OC = R  - радиус окружности, описанной около ΔABC
ΔAOD - прямоугольный: ∠AOD = 90°; ∠DAO = 45°; DO = 18 см  ⇒
∠ADO = 90° - ∠DAO = 90° - 45° = 45° = ∠DAO  ⇒
ΔAOD - прямоугольный равнобедренный ⇒ 
AO = DO = 18 см - радиус описанной окружности  R ⇒
AB = BC  = AC = a = R√3 = 18√3 см

Площадь равностороннего треугольника
$S_o= \frac{a^2 \sqrt{3} }{4} = \frac{(18 \sqrt{3} )^2 \sqrt{3} }{4} = \frac{324*3 \sqrt{3} }{4} =243 \sqrt{3}$ см²
Площадь основания   243√3 см² ≈ 420,9 см²