Предмет: Алгебра,
автор: Таня09091
в треугольнике АВС известно, что аб=бс=25; ас=14. Найдите дианы вм
Приложения:
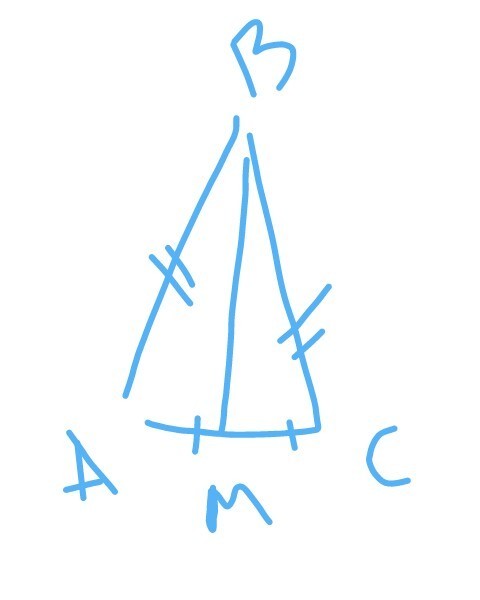
Ответы
Автор ответа:
1
ΔABC-равнобедренный. AC = 14 см., тогда AM=AC=7. По теореме Пифагора можем вычислить катет, т.е. BM.
 см.
см.
Автор ответа:
1
Дано:
АВ=ВС=25(треугольник АВС - равнобедренный)
АС=14
Найти:
ВМ
Решение:
Медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой.
Получим треугольники АМВ и ВМС .
Рассмотрим треугольник АМВ. Он прямоугольный ( угол АМВ = 90 градусов, АВ - гипотенуза)
Воспользуемся Теоремой Пифагора:
АВ^2 = AM^2 + BM^2
BM^2 = AB^2 - AM^2
BM^2 = 25^2 - 7^2
BM^2=625-49
BM = √576 = 24(cм)
Ответ: 24 см
АВ=ВС=25(треугольник АВС - равнобедренный)
АС=14
Найти:
ВМ
Решение:
Медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой.
Получим треугольники АМВ и ВМС .
Рассмотрим треугольник АМВ. Он прямоугольный ( угол АМВ = 90 градусов, АВ - гипотенуза)
Воспользуемся Теоремой Пифагора:
АВ^2 = AM^2 + BM^2
BM^2 = AB^2 - AM^2
BM^2 = 25^2 - 7^2
BM^2=625-49
BM = √576 = 24(cм)
Ответ: 24 см
Похожие вопросы
Предмет: Информатика,
автор: udontknowme5
Предмет: Русский язык,
автор: Аноним
Предмет: Геометрия,
автор: pankration20let
Предмет: Алгебра,
автор: школник0
Предмет: Обществознание,
автор: masharepina