Предмет: Алгебра,
автор: mashakolachuk1
Hайти производную функции..........
Приложения:
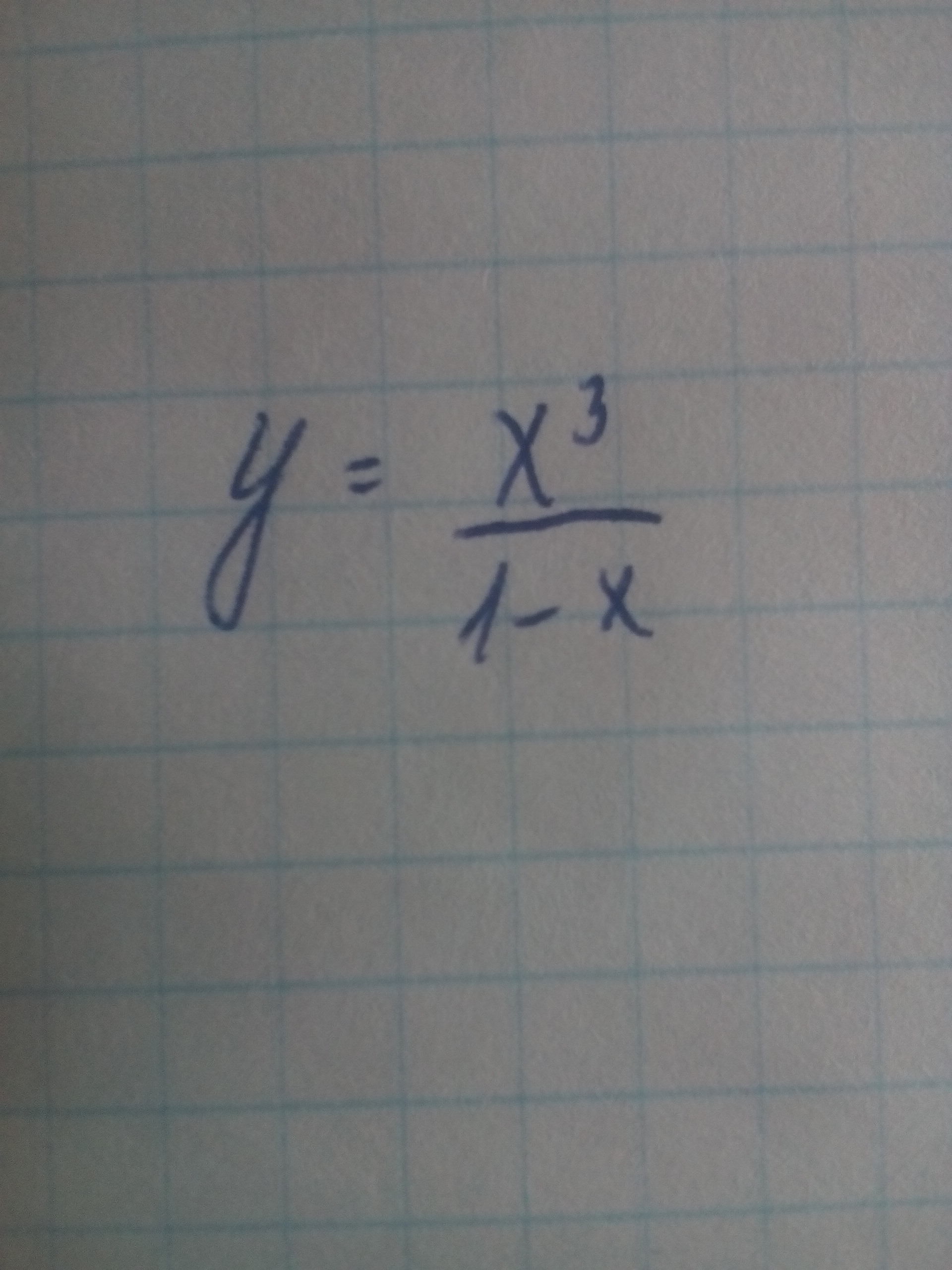
Ответы
Автор ответа:
0
Общая формула:
(p/q)'=(p'q - pq')/q²
Применение:
(x³/(1-x))'=((x³)' * (1-x) - (1-x)' * x³)/(1-x)²
Общая формула:
(x^n)'=nx^(n-1)
Применение:
=(3x²(1-x) - (1-x)' * x³)/(1-x)²
Общая формула и свойство:
(p-q)'=p'-q'
1'=0
Применение:
=(3x²(1-x) +x° * x³)/(1-x)²=(3x²(1-x)+x³)/(1-x)²=(3x²-2x³)/(1-x)²
(3x²-2x³)/(1-2x+x²)
Ответ: у=(3x²-2x³)/(1-2x+x²)
(p/q)'=(p'q - pq')/q²
Применение:
(x³/(1-x))'=((x³)' * (1-x) - (1-x)' * x³)/(1-x)²
Общая формула:
(x^n)'=nx^(n-1)
Применение:
=(3x²(1-x) - (1-x)' * x³)/(1-x)²
Общая формула и свойство:
(p-q)'=p'-q'
1'=0
Применение:
=(3x²(1-x) +x° * x³)/(1-x)²=(3x²(1-x)+x³)/(1-x)²=(3x²-2x³)/(1-x)²
(3x²-2x³)/(1-2x+x²)
Ответ: у=(3x²-2x³)/(1-2x+x²)
Похожие вопросы
Предмет: Физика,
автор: aituarakylbekov8
Предмет: Математика,
автор: Аноним
Предмет: Окружающий мир,
автор: elizavetagacenko13
Предмет: Физика,
автор: Milka5050
Предмет: Математика,
автор: Альберт11111111