Предмет: Алгебра,
автор: zrfnzk
Помогите срочно. Очень много баллов. Решите уравнения
Приложения:
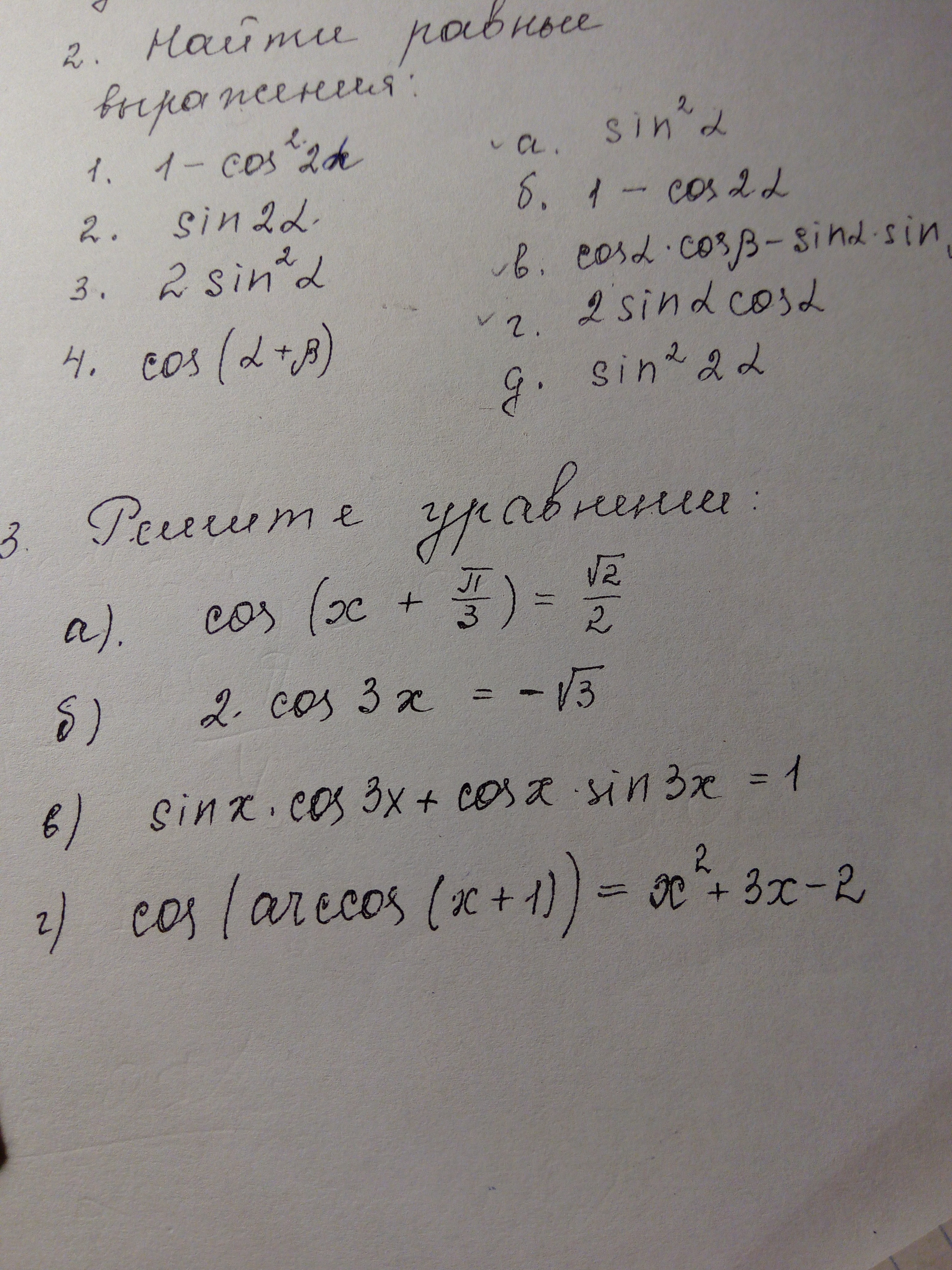
Godnessgirl:
а первое надо делать?
Ответы
Автор ответа:
1
3а


везде после n через запятую пишем nєZ.
3б
2cos(3x)=-√3

3в
sin(x)cos(3x)+cos(x)sin(3x)=1
sin(4x)=1

3г
cos(arccos(x+1))=х²+3х-2
одз: |х+1|≤1
-1≤х+1≤1
-2≤х≤0
хє[-2;0]
х+1=х²+3х-2
х²+2х-3=0
т. к. а+b+c=0 (1+2-3=0), то х1=1, х2=с/а, т.е.
х1=1
х2=-3 не пренадлежит [-2;0] и не удовлетворяет одз.
ответ х=1.
2. на всякий случай
1д
2г
3б
4в
везде после n через запятую пишем nєZ.
3б
2cos(3x)=-√3
3в
sin(x)cos(3x)+cos(x)sin(3x)=1
sin(4x)=1
3г
cos(arccos(x+1))=х²+3х-2
одз: |х+1|≤1
-1≤х+1≤1
-2≤х≤0
хє[-2;0]
х+1=х²+3х-2
х²+2х-3=0
т. к. а+b+c=0 (1+2-3=0), то х1=1, х2=с/а, т.е.
х1=1
х2=-3 не пренадлежит [-2;0] и не удовлетворяет одз.
ответ х=1.
2. на всякий случай
1д
2г
3б
4в
Спасибо, выручила
Похожие вопросы
Предмет: Музыка,
автор: elvira9023
Предмет: Русский язык,
автор: nastysha6733
Предмет: Физика,
автор: PR0BIRKA
Предмет: Математика,
автор: Dorian04