Question

!!!ПОМОГИТЕ ПОЖАЛУЙСТА!!!
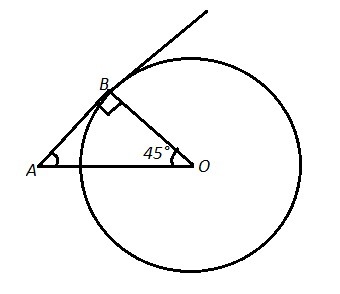
К окружности с центром О провели касательную АВ (В-точка касания). Найдите радиус окружности, если АВ=8см и (угол) AOB=45°

Answer 1

Так как ∠АОВ=45°  и ΔАОВ - прямоугольный (∠АВО=90°, т.к. радиус окружности , проведённый в точку касания , перпендикулярен касательной), то и ∠ВАО=45°,
а значит ΔАОВ равнобедренный  ⇒
АВ=ОВ=8 см
Но ОВ= радиусу окружности  ⇒  R=8 cм.