Question

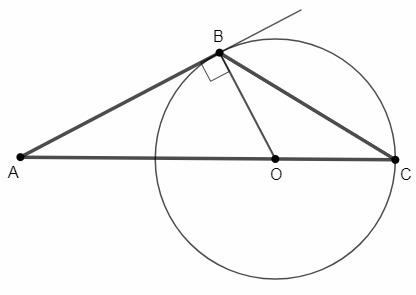
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB = 15, AC = 25.

Answer 1

OB=OC=r
AO=AC-OC =25-r

Радиус, проведенный в точку касания, перпендикулярен касательной.
∠ABO=90°

AO^2= AB^2 +OB^2 <=>
(25-r)^2= 15^2 +r^2 <=>
25^2 -50r +r^2 = 15^2 +r^2 <=>
r =(25^2 -15^2)/50 =10*40/50 =8

D=2r=16