Предмет: Геометрия,
автор: nadau
Помогите срочно, пожалуйста!))!!
1.В равнобедренном треугольнике вписана окружность, которая точкой касания делит боковую сторону на отрезки длиной 18 и 16 см, считая от вершина. Найдите радиус вписанной окружности и площадь треугольника
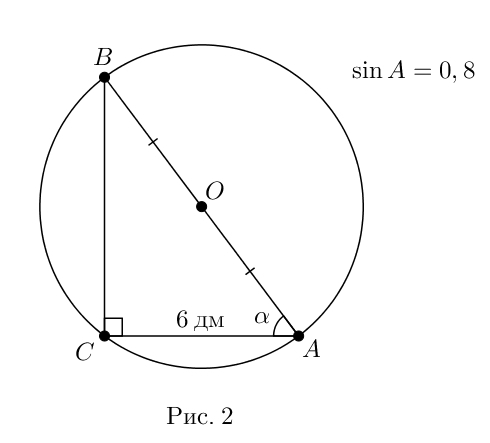
2.Прямоугольный треугольник вписан в окружность. Найдите радиус этой окружности, если катет треугольника равен 6дм, а синус прилежащего угла равен 0.8
3.Докажите, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.
Kазак:
Пачка заданий = кратчайший путь остаться без ответа
Ответы
Автор ответа:
5
Задача №1
Отрезки, соединяющие вершины треугольника с точками касания вписанной окружности, равны (свойство касательных). Следовательно,
 (см. рис. 1). Поэтому сторона AB равна 16+16=32.
(см. рис. 1). Поэтому сторона AB равна 16+16=32.
Найдём полупериметр p:

Теперь найдём площадь по формуле Герона:

Теперь по формуле найдём радиус вписанной окружности:
найдём радиус вписанной окружности:

Ответ: площадь — 480 см², радиус вп. окружности — 9,6 см.
Задача №2
Cм. рис. 2. O — центр описанной окружности, A — прилежащий угол.
Найдём синус противолежащего угла:

Теперь найдём гипотенузу, применив теорему синусов:

Радиус R описанной окружности в прямоугольном треугольнике равен половине гипотенузы, поэтому:

Ответ: 5 дм (не см!!!)
Задача №3
См. рис. 3. BC || AD, AB и CD — бёдра трапеции. Докажем, что AB=CD.
Если вокруг четырёхугольника можно описать окружность, то сумма противоположных углов равна 180° (необходимое условие). То есть ∠A+∠C=∠B+∠D=180°.
С другой стороны, сумма углов, прилежащих к боковым сторонам трапеции, равна 180° (по теореме о параллельных прямых BC и AD и секущей AB). Следовательно, ∠A+∠B=∠C+∠D=180°.
Сопоставив эти равенства, получим, что ∠A=∠D и ∠B=∠C. Является ли это доказательством, что трапеция равнобедренная? Я не помню, изучают ли в школе эту теорему, поэтому на всякий случай докажу.
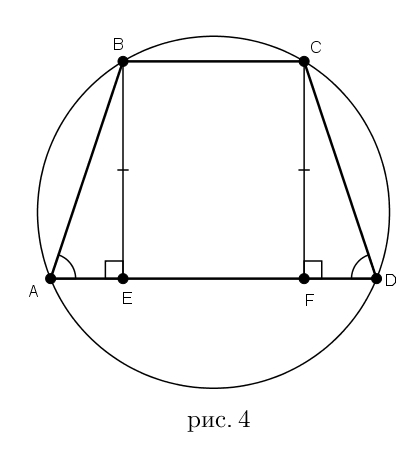
Проведём высоты BE и CF (см. рис. 4). Они равны, так как все высоты трапеции равны. Поэтому прямоугольные треугольники ABE и DFC равны (по острому углу и катету). Значит, равны их гипотенузы — AB и CD, что и требовалось доказать.
Отрезки, соединяющие вершины треугольника с точками касания вписанной окружности, равны (свойство касательных). Следовательно,
Найдём полупериметр p:
Теперь найдём площадь по формуле Герона:
Теперь по формуле
Ответ: площадь — 480 см², радиус вп. окружности — 9,6 см.
Задача №2
Cм. рис. 2. O — центр описанной окружности, A — прилежащий угол.
Найдём синус противолежащего угла:
Теперь найдём гипотенузу, применив теорему синусов:
Радиус R описанной окружности в прямоугольном треугольнике равен половине гипотенузы, поэтому:
Ответ: 5 дм (не см!!!)
Задача №3
См. рис. 3. BC || AD, AB и CD — бёдра трапеции. Докажем, что AB=CD.
Если вокруг четырёхугольника можно описать окружность, то сумма противоположных углов равна 180° (необходимое условие). То есть ∠A+∠C=∠B+∠D=180°.
С другой стороны, сумма углов, прилежащих к боковым сторонам трапеции, равна 180° (по теореме о параллельных прямых BC и AD и секущей AB). Следовательно, ∠A+∠B=∠C+∠D=180°.
Сопоставив эти равенства, получим, что ∠A=∠D и ∠B=∠C. Является ли это доказательством, что трапеция равнобедренная? Я не помню, изучают ли в школе эту теорему, поэтому на всякий случай докажу.
Проведём высоты BE и CF (см. рис. 4). Они равны, так как все высоты трапеции равны. Поэтому прямоугольные треугольники ABE и DFC равны (по острому углу и катету). Значит, равны их гипотенузы — AB и CD, что и требовалось доказать.
Приложения:


Похожие вопросы
Предмет: Қазақ тiлi,
автор: kuanyshnurkhat
Предмет: Қазақ тiлi,
автор: maratkanagatov8
Предмет: Информатика,
автор: supersonichedgehog
Предмет: Математика,
автор: tau214
Предмет: История,
автор: НацуДрагнил22