Умоляю, решите!!! 30 Баллов!!!
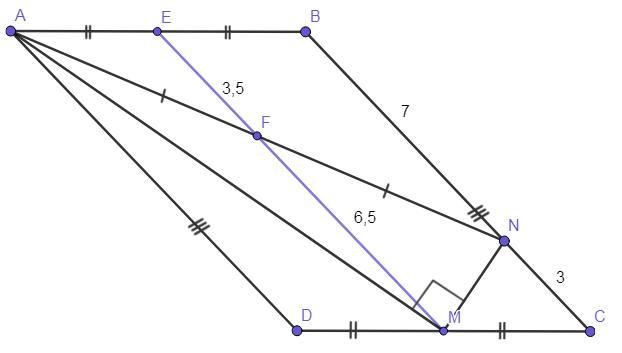
В четырёхугольнике ABCD стороны AD и BC равны и параллельны. Точка M — середина стороны CD, точка N на стороне BC такова, что ∠AMN=90 ∘ . Известно, что BN=7, NC=3. Чему равна длина отрезка AN?
Ответы
Чертёж смотрите во вложении.
Дано:
ABCD - четырёхугольник.
AD = BC.
AD║BC.
Точка М - середина CD.
Точка N ∈ ВС.
BN = 7.
CN = 3.
∠AMN = 90°.
Найти:
AN = ?
Решение:
Так как AD = BC и AD║BC, то четырёхугольник ABCD - параллелограмм (по признаку параллелограмма).
Если на одной из двух прямых последовательно отметь несколько равных отрезков и через их концы провести параллельные прямые, то они отсекут на второй прямой равные между собой отрезки (теорема Фалеса). Проведём через точку М прямую МЕ, которая параллельна AD и пересекает сторону AN в точке F. Так как МЕ║AD и AD║ВС, то также МЕ║AD║ВС. Следовательно, по теореме Фалеса, AF = NF, AE = ЕВ.
Рассмотрим четырёхугольник ЕВСМ. Так как ЕМ║ВС (по выше доказанному) и отрезки ЕВ║МС (так как лежат на параллельных прямых), то четырёхугольник ЕВСМ - параллелограмм по определению. Тогда, по свойству параллелограмма, ВС = ЕМ = BN+NC = 7+3 = 10.
Рассмотрим ΔABN. Так как отрезок EF соединяет середины сторон АВ и AN, то EF - средняя линия, причём параллельна стороне BN, а значит, равна её половине (по свойству средней линии треугольника). EF = BN/2 = 7/2 = 3,5.
ЕМ = EF+FM ⇒ FM = ЕМ-EF ⇒ FM = 10-3,5 = 6,5.
Рассмотрим ΔANM - прямоугольный (по условию). FM - медиана, проведённая к гипотенузе, а значит, равна её половине (по свойству прямоугольного треугольника). AN = 2*FM ⇒ AN = 2*6,5 ⇒ AN = 13.
Ответ: 13.