Предмет: Алгебра,
автор: Аноним
Вот ещё 7 интегралов для решеня
Приложения:
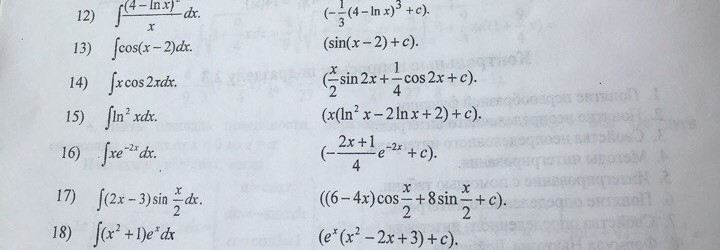
Ответы
Автор ответа:
0
(12)
![\int\limits {\frac{[4-ln(x)]^2}{x}} \, dx = \int\limits {[4-ln(x)]^2*\frac{1}{x}} \, dx =\\\\ = \int\limits {[4-ln(x)]^2} \, d[ln(x)] = -\int\limits {[4-ln(x)]^2} \, d[-ln(x)] =\\\\ = -\int\limits {[4-ln(x)]^2} \, d[4-ln(x)] =-\frac{[4-ln(x)]^3}{3}+C \int\limits {\frac{[4-ln(x)]^2}{x}} \, dx = \int\limits {[4-ln(x)]^2*\frac{1}{x}} \, dx =\\\\ = \int\limits {[4-ln(x)]^2} \, d[ln(x)] = -\int\limits {[4-ln(x)]^2} \, d[-ln(x)] =\\\\ = -\int\limits {[4-ln(x)]^2} \, d[4-ln(x)] =-\frac{[4-ln(x)]^3}{3}+C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7B%5Cfrac%7B%5B4-ln%28x%29%5D%5E2%7D%7Bx%7D%7D+%5C%2C+dx+%3D+%5Cint%5Climits+%7B%5B4-ln%28x%29%5D%5E2%2A%5Cfrac%7B1%7D%7Bx%7D%7D+%5C%2C+dx+%3D%5C%5C%5C%5C+%3D+%5Cint%5Climits+%7B%5B4-ln%28x%29%5D%5E2%7D+%5C%2C+d%5Bln%28x%29%5D+%3D+-%5Cint%5Climits+%7B%5B4-ln%28x%29%5D%5E2%7D+%5C%2C+d%5B-ln%28x%29%5D+%3D%5C%5C%5C%5C+%3D+-%5Cint%5Climits+%7B%5B4-ln%28x%29%5D%5E2%7D+%5C%2C+d%5B4-ln%28x%29%5D+%3D-%5Cfrac%7B%5B4-ln%28x%29%5D%5E3%7D%7B3%7D%2BC)
(13)

(14)
![\int\limits {xcos(2x)} \, dx =\frac{1}{2} \int\limits {x*2cos(2x)} \, dx =\\\\ =\frac{1}{2} \int\limits {x} \, d(sin(2x)) =\frac{1}{2}*[x*sin(2x)- \int\limits {sin(2x)} \, dx ]=\\\\ =\frac{1}{2}*[x*sin(2x)- \frac{1}{2}*\int\limits {sin(2x)} \, d(2x) ]=\\\\ =\frac{1}{2}*[x*sin(2x)+ \frac{1}{2}*cos(2x)]+C=\\\\ =\frac{x*sin(2x)}{2}+\frac{cos(2x)}{4}+C \int\limits {xcos(2x)} \, dx =\frac{1}{2} \int\limits {x*2cos(2x)} \, dx =\\\\ =\frac{1}{2} \int\limits {x} \, d(sin(2x)) =\frac{1}{2}*[x*sin(2x)- \int\limits {sin(2x)} \, dx ]=\\\\ =\frac{1}{2}*[x*sin(2x)- \frac{1}{2}*\int\limits {sin(2x)} \, d(2x) ]=\\\\ =\frac{1}{2}*[x*sin(2x)+ \frac{1}{2}*cos(2x)]+C=\\\\ =\frac{x*sin(2x)}{2}+\frac{cos(2x)}{4}+C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7Bxcos%282x%29%7D+%5C%2C+dx+%3D%5Cfrac%7B1%7D%7B2%7D+%5Cint%5Climits+%7Bx%2A2cos%282x%29%7D+%5C%2C+dx+%3D%5C%5C%5C%5C+%3D%5Cfrac%7B1%7D%7B2%7D+%5Cint%5Climits+%7Bx%7D+%5C%2C+d%28sin%282x%29%29+%3D%5Cfrac%7B1%7D%7B2%7D%2A%5Bx%2Asin%282x%29-+%5Cint%5Climits+%7Bsin%282x%29%7D+%5C%2C+dx+%5D%3D%5C%5C%5C%5C+%3D%5Cfrac%7B1%7D%7B2%7D%2A%5Bx%2Asin%282x%29-+%5Cfrac%7B1%7D%7B2%7D%2A%5Cint%5Climits+%7Bsin%282x%29%7D+%5C%2C+d%282x%29+%5D%3D%5C%5C%5C%5C+%3D%5Cfrac%7B1%7D%7B2%7D%2A%5Bx%2Asin%282x%29%2B+%5Cfrac%7B1%7D%7B2%7D%2Acos%282x%29%5D%2BC%3D%5C%5C%5C%5C+%3D%5Cfrac%7Bx%2Asin%282x%29%7D%7B2%7D%2B%5Cfrac%7Bcos%282x%29%7D%7B4%7D%2BC)
(15)
![\int\limits {ln^2(x)} \, dx =x*ln^2(x)- \int\limits {x*} \, d[ln^2(x)] =\\\\ =x*ln^2(x)- \int\limits {x*2ln(x)*\frac{1}{x}} \, dx =\\\\ =x*ln^2(x)- 2*\int\limits {ln(x)} \, dx =\\\\ =x*ln^2(x)- 2*[x*ln(x)-\int\limits {x} \, d[ln(x)]] =\\\\ =x*ln^2(x)- 2*[x*ln(x)-\int\limits {x*\frac{1}{x}} \, dx] =\\\\ =x*ln^2(x)- 2x*ln(x)+2\int\limits {1} \, dx=\\\\ =x*ln^2(x)- 2x*ln(x)+2x+C=\\\\ =x*(ln^2(x)- 2ln(x)+2)+C \int\limits {ln^2(x)} \, dx =x*ln^2(x)- \int\limits {x*} \, d[ln^2(x)] =\\\\ =x*ln^2(x)- \int\limits {x*2ln(x)*\frac{1}{x}} \, dx =\\\\ =x*ln^2(x)- 2*\int\limits {ln(x)} \, dx =\\\\ =x*ln^2(x)- 2*[x*ln(x)-\int\limits {x} \, d[ln(x)]] =\\\\ =x*ln^2(x)- 2*[x*ln(x)-\int\limits {x*\frac{1}{x}} \, dx] =\\\\ =x*ln^2(x)- 2x*ln(x)+2\int\limits {1} \, dx=\\\\ =x*ln^2(x)- 2x*ln(x)+2x+C=\\\\ =x*(ln^2(x)- 2ln(x)+2)+C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7Bln%5E2%28x%29%7D+%5C%2C+dx+%3Dx%2Aln%5E2%28x%29-+%5Cint%5Climits+%7Bx%2A%7D+%5C%2C+d%5Bln%5E2%28x%29%5D+%3D%5C%5C%5C%5C+%3Dx%2Aln%5E2%28x%29-+%5Cint%5Climits+%7Bx%2A2ln%28x%29%2A%5Cfrac%7B1%7D%7Bx%7D%7D+%5C%2C+dx+%3D%5C%5C%5C%5C+%3Dx%2Aln%5E2%28x%29-+2%2A%5Cint%5Climits+%7Bln%28x%29%7D+%5C%2C+dx+%3D%5C%5C%5C%5C+%3Dx%2Aln%5E2%28x%29-+2%2A%5Bx%2Aln%28x%29-%5Cint%5Climits+%7Bx%7D+%5C%2C+d%5Bln%28x%29%5D%5D+%3D%5C%5C%5C%5C+%3Dx%2Aln%5E2%28x%29-+2%2A%5Bx%2Aln%28x%29-%5Cint%5Climits+%7Bx%2A%5Cfrac%7B1%7D%7Bx%7D%7D+%5C%2C+dx%5D+%3D%5C%5C%5C%5C+%3Dx%2Aln%5E2%28x%29-+2x%2Aln%28x%29%2B2%5Cint%5Climits+%7B1%7D+%5C%2C+dx%3D%5C%5C%5C%5C+%3Dx%2Aln%5E2%28x%29-+2x%2Aln%28x%29%2B2x%2BC%3D%5C%5C%5C%5C+%3Dx%2A%28ln%5E2%28x%29-+2ln%28x%29%2B2%29%2BC)
(16)
![\int\limits {xe^{-2x}} \, dx = \int\limits {x} \, d(\frac{e^{-2x}}{-2}) =-\frac{1}{2}* \int\limits {x} \, d(e^{-2x}) =\\\\ =-\frac{1}{2}*[x*e^{-2x}- \int\limits {e^{-2x}} \, dx ]=\\\\ =-\frac{1}{2}*[x*e^{-2x}+\frac{1}{2} *\int\limits {e^{-2x}} \, d(-2x) ]=\\\\ =-\frac{1}{2}*[x*e^{-2x}+\frac{1}{2} *e^{-2x} ]+C=\\\\ =-\frac{e^{-2x}}{2}*[x+\frac{1}{2}]+C=\\\\ =-\frac{2x+1}{4}*e^{-2x}+C \int\limits {xe^{-2x}} \, dx = \int\limits {x} \, d(\frac{e^{-2x}}{-2}) =-\frac{1}{2}* \int\limits {x} \, d(e^{-2x}) =\\\\ =-\frac{1}{2}*[x*e^{-2x}- \int\limits {e^{-2x}} \, dx ]=\\\\ =-\frac{1}{2}*[x*e^{-2x}+\frac{1}{2} *\int\limits {e^{-2x}} \, d(-2x) ]=\\\\ =-\frac{1}{2}*[x*e^{-2x}+\frac{1}{2} *e^{-2x} ]+C=\\\\ =-\frac{e^{-2x}}{2}*[x+\frac{1}{2}]+C=\\\\ =-\frac{2x+1}{4}*e^{-2x}+C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7Bxe%5E%7B-2x%7D%7D+%5C%2C+dx+%3D+%5Cint%5Climits+%7Bx%7D+%5C%2C+d%28%5Cfrac%7Be%5E%7B-2x%7D%7D%7B-2%7D%29+%3D-%5Cfrac%7B1%7D%7B2%7D%2A+%5Cint%5Climits+%7Bx%7D+%5C%2C+d%28e%5E%7B-2x%7D%29+%3D%5C%5C%5C%5C+%3D-%5Cfrac%7B1%7D%7B2%7D%2A%5Bx%2Ae%5E%7B-2x%7D-+%5Cint%5Climits+%7Be%5E%7B-2x%7D%7D+%5C%2C+dx+%5D%3D%5C%5C%5C%5C+%3D-%5Cfrac%7B1%7D%7B2%7D%2A%5Bx%2Ae%5E%7B-2x%7D%2B%5Cfrac%7B1%7D%7B2%7D+%2A%5Cint%5Climits+%7Be%5E%7B-2x%7D%7D+%5C%2C+d%28-2x%29+%5D%3D%5C%5C%5C%5C+%3D-%5Cfrac%7B1%7D%7B2%7D%2A%5Bx%2Ae%5E%7B-2x%7D%2B%5Cfrac%7B1%7D%7B2%7D+%2Ae%5E%7B-2x%7D+%5D%2BC%3D%5C%5C%5C%5C+%3D-%5Cfrac%7Be%5E%7B-2x%7D%7D%7B2%7D%2A%5Bx%2B%5Cfrac%7B1%7D%7B2%7D%5D%2BC%3D%5C%5C%5C%5C+%3D-%5Cfrac%7B2x%2B1%7D%7B4%7D%2Ae%5E%7B-2x%7D%2BC)
(17)
![\int\limits {(2x-3)*sin(\frac{x}{2})} \, dx = \int\limits {(2x-3)} \, d[-2cos(\frac{x}{2})] =\\\\ =-2cos(\frac{x}{2})*(2x-3)- \int\limits {[-2cos(\frac{x}{2})]} \, d(2x-3) =\\\\ =-2cos(\frac{x}{2})*(2x-3)+4\int\limits {cos(\frac{x}{2})} \, dx =\\\\ =-2cos(\frac{x}{2})*(2x-3)+8\int\limits {cos(\frac{x}{2})} \, d(\frac{x}{2}) =\\\\ =-2cos(\frac{x}{2})*(2x-3)+8sin(\frac{x}{2})+C=\\\\ =(6-4x)*cos(\frac{x}{2})+8sin(\frac{x}{2})+C \int\limits {(2x-3)*sin(\frac{x}{2})} \, dx = \int\limits {(2x-3)} \, d[-2cos(\frac{x}{2})] =\\\\ =-2cos(\frac{x}{2})*(2x-3)- \int\limits {[-2cos(\frac{x}{2})]} \, d(2x-3) =\\\\ =-2cos(\frac{x}{2})*(2x-3)+4\int\limits {cos(\frac{x}{2})} \, dx =\\\\ =-2cos(\frac{x}{2})*(2x-3)+8\int\limits {cos(\frac{x}{2})} \, d(\frac{x}{2}) =\\\\ =-2cos(\frac{x}{2})*(2x-3)+8sin(\frac{x}{2})+C=\\\\ =(6-4x)*cos(\frac{x}{2})+8sin(\frac{x}{2})+C](https://tex.z-dn.net/?f=+%5Cint%5Climits+%7B%282x-3%29%2Asin%28%5Cfrac%7Bx%7D%7B2%7D%29%7D+%5C%2C+dx+%3D+%5Cint%5Climits+%7B%282x-3%29%7D+%5C%2C+d%5B-2cos%28%5Cfrac%7Bx%7D%7B2%7D%29%5D+%3D%5C%5C%5C%5C+%3D-2cos%28%5Cfrac%7Bx%7D%7B2%7D%29%2A%282x-3%29-+%5Cint%5Climits+%7B%5B-2cos%28%5Cfrac%7Bx%7D%7B2%7D%29%5D%7D+%5C%2C+d%282x-3%29+%3D%5C%5C%5C%5C+%3D-2cos%28%5Cfrac%7Bx%7D%7B2%7D%29%2A%282x-3%29%2B4%5Cint%5Climits+%7Bcos%28%5Cfrac%7Bx%7D%7B2%7D%29%7D+%5C%2C+dx+%3D%5C%5C%5C%5C+%3D-2cos%28%5Cfrac%7Bx%7D%7B2%7D%29%2A%282x-3%29%2B8%5Cint%5Climits+%7Bcos%28%5Cfrac%7Bx%7D%7B2%7D%29%7D+%5C%2C+d%28%5Cfrac%7Bx%7D%7B2%7D%29+%3D%5C%5C%5C%5C+%3D-2cos%28%5Cfrac%7Bx%7D%7B2%7D%29%2A%282x-3%29%2B8sin%28%5Cfrac%7Bx%7D%7B2%7D%29%2BC%3D%5C%5C%5C%5C+%3D%286-4x%29%2Acos%28%5Cfrac%7Bx%7D%7B2%7D%29%2B8sin%28%5Cfrac%7Bx%7D%7B2%7D%29%2BC)
(18)

(13)
(14)
(15)
(16)
(17)
(18)
Похожие вопросы
Предмет: Русский язык,
автор: karakozbalysbekova
Предмет: География,
автор: hovrinartem37
Предмет: Русский язык,
автор: olesyaevtina
Предмет: Алгебра,
автор: Anna9856
Предмет: История,
автор: dan121222