Question

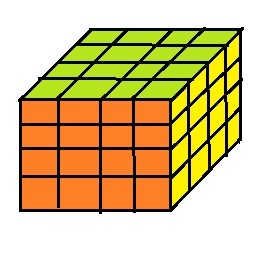
Куб со стороной 4 см покрашен в три разных цвета: красный синий и зеленый. Противоположные грани куба одинакового цвета. Куб разделили на 64 маленьких кубиков одинакового размера.
а) В скольких маленьких кубиках как минимум 2 покрашенных стороны?

б) Сколько таких кубиков у которых как минимум 1 покрашенная сторона?

в) Сколько кубиков без покрашенных сторон?

Answer 1

Чтобы разделить куб на 64 маленьких кубика, надо сделать по 4 разреза на каждой грани, получим 4*4*4=64 кубика.
3 окрашенные стороны у 8 угловых кубиков,
2 окрашенные стороны у 24 кубиков, прилегающих к рёбрам,
1 окрашенная сторона у 24 кубиков, находящихся по центру граней,
0 окрашенных сторон у 64-8-24-24=8 кубиков, находящихся внутри куба.
а) минимум 2 покрашенные стороны (две или три) у 32 кубиков,
б) минимум 1 покрашенная сторона (одна или две или три) у 56 кубиков,
в) не покрашены стороны у 8 кубиков.