Предмет: Алгебра,
автор: zhansayakomekova99
Помогите решить 2095, 2099, 2101
Приложения:
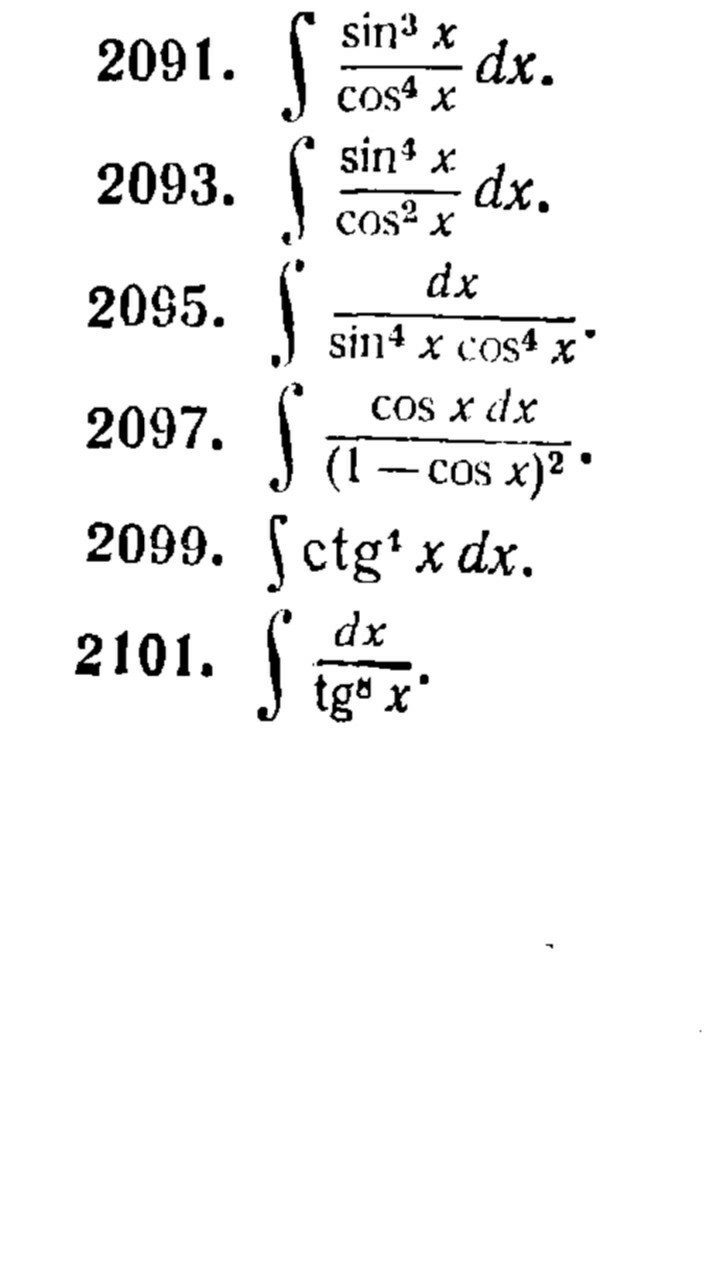
Ответы
Автор ответа:
0
2095

Дальше простой рациональный интеграл
2099 - не видно степень котангенса
2101

Дальше простой рациональный интеграл
Дальше простой рациональный интеграл
2099 - не видно степень котангенса
2101
Дальше простой рациональный интеграл
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Геометрия,
автор: Аноним
Предмет: Русский язык,
автор: xatfray
Предмет: Математика,
автор: sashadashko19